Мультипликативные обратные по модулю

Решая уравнение вида , приходим к вопросу о существовании мультипликативного обратного числа по модулю . Другими словами, необходимо выяснить, существует ли число , удовлетворяющее условиям . Для такого числа естественно обозначение .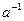

Обратный к элемент существует только тогда, когда НОД 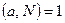. Особый интерес представляет случай простого модуля , поскольку при этом для любого ненулевого элемента найдется единственное решение уравнения . Таким образом, если - простое число, то любой ненулевой элемент в является обратимым, т. е. обладает обратным элементом.

Определение. Полем называется множество с двумя операциями, обладающее дополнительными свойствами:

1. - абелева группа с единичным элементом 0

2. - абелева группа с единичным элементом 1.

3. удовлетворяет закону дистрибутивности.

Другими словами, поле – это коммутативное кольцо, в котором каждый ненулевой элемент обратим.

Обозначим множество обратимых элементов в 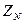как 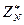, т. е. 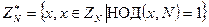. Для общего кольца обозначение закреплено для наибольшего его подмножества элементов, которые образуют группу по умножению.

В специальном случае, когда - простое число, получаем 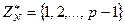, поскольку каждый ненулевой элемент кольца 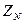взаимно прост с и поэтому обратим. Другими словами, 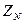является конечным полем, которое обычно называется полем вычетов по модулю и обозначается символом 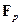. Из определения следует, что мультипликативная группа поля 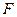совпадает с множеством 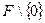. В частном случае поля вычетов получаем 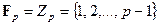и .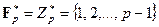

Замечание. Целые числа по модулю образуют поле тогда и только тогда, когда - простое число.