Основы теории групп
Определение. Полугруппой называется множество, в котором определено действие, ставящее в соответствие каждой упорядоченной паре элементов данного множества третий элемент из этого множества, называемый результатом действия.
Действие предполагается ассоциативным. Полугруппами являются множество целых неотрицательных чисел относительно действия сложения, это же множество относительно действия умножения, квадратные матрицы относительно действий сложения и умножения и т.д. Однако для матриц действие умножения не является коммутативным.
Определение. Группой называется полугруппа, если в ней существует нейтральный элемент 
такой, что для каждого элемента 
из группы 
(
- знак действия), и для каждого элемента существует обратный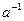 
такой, что 
.
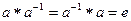Примерами групп могут служить множество целых чисел относительно сложения, множество положительных рациональных чисел относительно умножения, множество матриц размера 
относительно сложения. Все эти группы коммутативны.
Определение. Абелевыми группами называются коммутативные группы.
Действие в группе обозначается обычно как умножение (мультипликативная запись), иногда как сложение (аддитивная запись). Аддитивная запись применяется только для коммутативных групп. Нейтральный элемент при мультипликативной записи обозначается 1, при аддитивной записи 0. Соответственно, обратный к элемент в мультипликативной записи обозначается 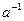, в аддитивной – через (
) и называется противоположным элементом.
Пусть 
- множество, в котором определена бинарная операция, которая каждой упорядоченной паре a, b элементов из М ставит в соответствие третий элемент – их произведение ab.
Теорема. Если действие в М ассоциативно, т. е. М – полугруппа, то произведение упорядоченной совокупности 
, 
,…, 
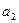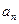элементов не зависит от способа расстановки скобок, т. е. от порядка выполнения бинарных операций.
Доказательство. Назовем произведение, в котором сомножители присоединяются последовательно по одному слева направо, левонормированным. Докажем по индукции, что произведение с любой расстановкой скобок равно левонормированному. Для 
это верно в силу ассоциативности. Пусть 
и это утверждение верно для произведений из 
элементов при 
. Рассмотрим произведение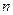 
элементов , ,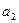…, 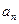с некоторой расстановкой скобок. Так как действий бинарно, то это произведение равно произведению двух сомножителей 
и 
с какими-то расстановками скобок. В силу индуктивного предположения эти сомножители являются левонормированнвми произведениями. Если 
, то рассматриваемое произведение равно 
и получается из левонормированного произведения 
присоединением справа еще одного сомножителя 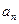, так что оно само левонормированное. Если же 
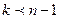, то 
= = 
= 
. В силу индуктивного предположения сомножитель 
равен левонормированному произведению 
, и после присоединения 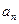справа получается снова левонормированное произведение. Теорема доказана.
Используя эту теорему, можно записывать произведение элементов в группе без расстановки скобок, указывающих порядок выполнения бинарной операции. В частности, произведение n равных сомножителей не зависит от способа расстановки скобок, поэтому имеет смысл выражение 
(или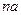 
при аддитивной записи) и 
.
