Китайская теорема об остатках (КТО) является очень древней находкой математики, которой около 2000 лет.
КТО утверждает, что система уравнений 
имеет единственное решение по модулю 
тогда и только тогда, когда 
и 
взаимно просты. Кроме того, она дает простой метод нахождения этого решения. Например, система 
будет иметь решением 
. Легко проверить, что это число будет решением данной системы уравнений. Но как оно было найдено?
Так как 
, то 
. С другой стороны, 
. Поэтому 
или 
. Поскольку НОД 
=НОД 
, можем решить последнее уравнение относительно 
. Имеем 
, следовательно, 
. Поэтому 
. Тогда 
.
Приведем общую схему решения системы двух уравнений, так как такая система имеет важное значение. Предположим, что числа и взаимно просты и дана система уравнений 
Сначала определим 
. Это сделать можно в силу предположения о взаимной простоте чисел и . Затем вычисляем 
. Решение по модулю 
задается формулой 
. Чтобы убедиться в верности метода, сделаем проверку 
, 
.
В общем случае КТО посвящена системе из более чем двух уравнений. Пусть 
и 
- числа, причем все 
взаимно просты. Нужно найти такой элемент 
, 
, что 
для всех 
. КТО гарантирует существование и единственность решения и дает ответ: 
, где 
, 
.
Пример. Решить систему уравнений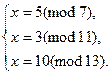 
Решение. Числа 7, 11, 13 взаимно простые, поэтому 
. Согласно выше изложенному методу 
, 
, 
, 
, 
, 
. Пользуясь формулой, получаем решение: 
.
