Для иллюстрации некоторых основных идей рассмотрим модель шарнира, содержащую одну степень свободы. Шарнир, связанный с упругой пружиной, можно рассматривать как простейшую модель стержня, закрепленного на одном конце (качественно он ведет себя как нижняя часть шарнирно опертого стержня).
Рисунок 1.35 - Статическое и динамическое поведение шарнирно опертого стержня с круговой пружиной
Рассмотрим невесомый недеформируемый стержень длиной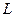 
, соединенный с упругой пружиной жесткости 
(см. рисунок). Пружина сопротивляется вращению стержня. Стержень несет точечную массу 
на конце и находится в постоянном гравитационном поле с ускорением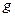 
, что означает, что консоль находится под действием силы величиной 
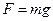. Мы будем рассматривать 
как управляющий параметр нагружения и будем исследовать потерю устойчивости системы по мере того, как постепенно увеличивается от нулевого значения.
Выберем в качестве обобщенной координаты угол поворота от вертикали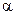 
и проведем сначала статический анализ.
Энергия деформации, накопленная в пружине, есть
,
а расстояние, на которое опустилась масса т, вычисляется по формуле 
.
Общая потенциальная энергия системы дается равенством
Уравнение равновесия
.
имеет тривиальное решение 
для всех и решение, определяемое из уравнения
Имеются две траектории равновесия. Они обозначены на рисунке жирными линиями. Устойчивость равновесных состояний определяется выражением
.
Вдоль основной «тривиальной» траектории равновесия устойчивость имеет место при , меньшем 
, а неустойчивость – при , большем , где 
. Предположим, что вал вращается с некоторой угловой частотой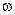 
, тогда выражение для силы будет иметь следующий вид 
.
Для устойчивого равновесного состояния имеем
и устойчивость имеет место при следующем критическом значении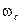 
равном
.
Аналогичным образом находятся устойчивые траектории равновесия в состоянии, превышающим критическое. Общая потенциальная энергия 
имеет единственный минимум для заданного 
и два минимума, разделенных максимумом, для каждого 
. Это схематически показано на рисунке.
Динамику системы в рамках нелинейной теории легко найти качественно при помощи графиков общей потенциальной энергии системы. Если пренебречь демпфированием, то центр, соответствующий тривиальному состоянию для , будет трансформироваться в два центра, разделенных седлом, для . Если имеется некоторая положительная вязкость, то устойчивый фокус в тривиальном состоянии для будет переходить в два устойчивых фокуса, разделенных седлом, как показано на рисунке для .
Мы не будем исследовать эти нелинейные движения и вместо этого рассмотрим линейные колебания около состояния равновесия . Будем считать, что стержень невесом. Тогда кинетическая энергия системы сводится к кинетической энергии точечной массы и дается формулой
.
Сравнивая ее с общим выражением для кинетической энергии
имеем 
. Угловая частота малых колебаний 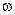тогда дается теорией линейного осциллятора в виде
Эта частота уменьшается до нуля, когда возрастает до . Мы видим, что имеются три различных пути для определения критической нагрузки :
(1) ветвление тривиальной траектории равновесия;
(2) исчезновение минимума потенциальной энергии;
(3) обращение в нуль частоты колебаний.
Эквивалентность (1) и (2) гарантируется основной теоремой теории упругой устойчивости. Эквивалентность (2) и (3) установлена для общих консервативных механических систем, в которых дополнительно учитывается малая вязкость.
В заключение рассмотрим влияние начальных геометрических несовершенств на изменение траектории статического равновесия системы. Предположим, что в силу небольшой технологической ошибки пружина находится в недеформированном состоянии не тогда, когда стержень вертикален, а когда он наклонен по отношению к вертикали на малый начальный угол 
. Общая потенциальная энергия системы с точностью до произвольной постоянной имеет теперь вид
,
поэтому для равновесия получим
,
что приводит к равенству
.
Видно, что траектория тривиального равновесия переходит в семейство равновесных кривых 
, соответствующих различным значениям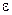 
и окружающих бифуркационные кривые идеальной системы, как показано на рисунке.