Изучим поведение стержня с точки зрения теории катастроф. Заменим наш стержень системой из двух жестких стержней шарнирными соединениями в точках А, В, С и пружиной в В, которая стремиться выпрямить шатуны в одну линию. Если пружина линейна, она создаст усилие 
, пропорциональное углу 
, и будет обладать потенциальной энергией 
, где 
– постоянная упругости пружины.
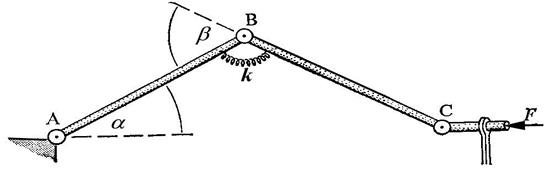
Рисунок 1.36 - Конечно-элементная модель стержня (2 стержня с пружиной)
Допустим, что каждое колено (шатун) имеет длину равную 1. Суммируя потенциальную энергию пружины и потенциальную энергию, отвечающую положению силы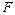 
, мы получим полную энергию (с точностью до константы)
.
Воспользуемся разложением в ряд Тейлора 
до четвертого порядка точности. В результате получим
.
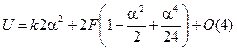откуда
.
Когда 
меньше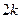 
, 
имеет минимум при 
(и нетрудно увидеть, что это единственный минимум).
Когда 
, имеет вырожденный минимум, в котором немедленно узнается точка стандартной сборки, так как коэффициент 
при 
положителен.
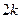Проводя через значение , скажем полагая 
, мы получим деформацию
.
Она универсальна среди четных функций (хотя мы и не дали алгебры, нужной для установления этого факта), и в действительности деформация исходной функции U сильно эквивалентна вблизи интересующей нас точки деформации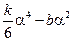 
диаграмма катастрофы для которой представлена на рисунке, а.
Рисунок 1.37 - Катастрофа сборки для модели стержня с одним шарниром
Но симметрия является здесь, неприемлемой как абсолютное ограничение, введение же почти любой асимметричной силы (рисунок 1.37 б) приводит нас к обычной картине сборки (рисунок 1.37 в). Для силы G такой, как показано на рисунке, имеем
так что
,
или
.
Отсюда следует, что U сильно эквивалентна
,
а это, с точностью до линейной замены, стандартная сборка.
В отличие от рассмотренного выше симметричного случая это описание структурно устойчиво. Возмутим функцию , заменив ее на 
, где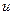 
– любая функция от 
и каких угодно других управляющих параметров, включенных в описание системы (разность длин шатунов, боковые смещения нагрузки 
, угол между и перпендикуляром к ). Тогда при малых значениях 
и прочих дополнительных параметров сохраняется не только та же картинка, но и та же формула, с точностью до гладкой замены переменных. Точка острия, направление острия и прочие параметры перемещаются плавно с изменением и дополнительных параметров. Это – следствие универсальности трансверсальных деформаций и устойчивости трансверсальности.
