В некотором отношении более поучительно рассмотреть пример неустойчивости, так как всегда легче увидеть неполадки, а затем можно сказать, что «устойчивость – это когда такое не случается».
Если бы, скажем, мы провели исследование машины Зимана лишь для управляющих точек 
на оси 
, то мы пришли бы к семейству функций
.
Критические точки находятся здесь из уравнения
,
они лежат на прямой 
и параболе 
, как это показано на рисунке а. Эта диаграмма часто встречается в книгах по теории бифуркаций. Для многих целей это описание может оказаться вполне адекватным. Однако оно не является структурно устойчивым и не позволяет охватить все моменты поведения машины. Например, на рисунке а при использовании принципа промедления мы не получим никаких катастрофических скачков.
Действительно, возмутим семейство приведенных функций малым членом 
, что дает
.
Теперь критические точки находятся из уравнения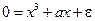 
, и соответствующий график (для малых ненулевых 
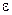) выглядит примерно так, как показано на рисунке б. Топология этого графика совсем другая. Например, он несвязен и не имеет точек самопересечения. Это верно для сколь угодно малых .
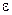Рисунок 1.32 - Структурная устойчивость семейств:
а – семейство кананических точек;
б – семейство канонических точек с учетом малых возмущених;
в – эксперимент
Имеет это значение или нет, зависит, конечно, от точной постановки вопроса, на который ищется ответ. Рисунок б служит хорошим приближением к рисунку а в других, нетопологических смыслах. Например, оба они очень похожи на рисунке в, который может принадлежать как раз к тому типу, который желают получить в эксперименте!
Дело, однако, в том, что мы не можем пренебречь структурной неустойчивостью с самого начала; прежде чем убедиться в ее безвредности, нужно проанализировать ее влияние на интересующие нас свойства. Например, от структурной неустойчивости функции 
, нельзя избавиться при помощи диаграммы вроде той, что показана на рисунке.
С другой стороны, полное семейство катастрофы сборки
является структурно устойчивым. В его правдоподобии можно убедиться при помощи следующего очень грубого рассуждения:
- возмущения порядка выше четвертого не должны оказывать никакого качественного влияния;
- члены четвертого порядка, квадратичные и линейные и так учитываются;
- кубические члены можно устранить подходящей заменой координат, как это делалось при анализе машины Зимана;
- наконец, постоянные не влияют на критические точки.
Сделать это рассуждение чем-то большим, чем благое пожелание, вероятно, невозможно, так как оно не учитывает всех имеющихся здесь трудностей; строгое доказательство совсем другое и лежит глубже.
Из структурной устойчивости катастрофы сборки следует, в частности, что малые погрешности при построении машины Зимана не должны заметно влиять на ее поведение. Эксперимент показывает, что даже очень большие погрешности могут не приводить ни к чему плохому. Иногда локальное менее локально, чем это ожидают.
