Симметричное и несимметричное прощелкивание арок
Рассмотрим теперь несколько иные эксперименты. Если изогнуть прямой упругий стержень и связать его концы сильно растянутой пружиной, то получится лук или пологая арка. Будем считать, что арка в состоянии проходить «сквозь» пружину, и одно возможное практическое устройство, использующее две симметрично расположенные пружины и обладающее этим свойством, показано на рисунке.
Прежде всего заметим, что при отсутствии вертикальной поперечной нагрузки эта предварительно напряженная механическая система имеет три возможных равновесных состояния. Во-первых, стержень может быть расположен так, что он изогнут либо вверх, либо вниз, – это дает два устойчивых состояния равновесия А и С на рисунке 1.42.
Кроме того, осторожно подталкивая стержень, мы можем привести его в равновесное состояние, которое является неустойчивым и в котором стержень прямой, а пружина сильно растянута; при этом стержень сжат нагрузкой, гораздо большей, чем критическая нагрузка Эйлера.
Рисунок 1.42 - Физическая модель арки, концы которой скреплены пружиной
Если теперь приложить мертвую поперечную нагрузку 
, то будут наблюдаться равновесные состояния, которым соответствует петля гистерезиса, изображенная на рисунке 1.43. Здесь два динамических перескока возвращают арку обратно в состояние А после того, как приложенная нагрузка проходит полный замкнутый цикл, включающий отрицательные значения 
.
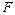Рисунок 1.43 - Симметричные деформации пологой арки с концами, соединенными пружиной
Перескоки происходят в двух складках или предельных точках D и Е. Отметим, что при прохождении мертвой приложенной нагрузкой замкнутого цикла область траектории неустойчивого равновесия, изображенная штрихами между этими двумя критическими состояниями, экспериментально не наблюдается. Эта область может фактически стать устойчивой и наблюдаться при жестком нагружении, в котором значения перемещения 
задаются при помощи червячной передачи.
В рассмотренном простом явлении траектория деформации арки ADBECF всегда симметрична относительно центральной оси О–О. Если, однако, сделать арку не очень пологой, она будет терять устойчивость по второй гармонике прежде, чем нагрузка достигнет точки максимума D, как изображено на рисунке. Поэтому возникнет несимметричная деформация, измеряемая величиной 
и арка последует по траектории равновесия, показанной в трех измерениях.
Для нагрузки, при которой не пологая арка должна совершить динамический скачок из состояния G в состояние Н, основная траектория с 
теряет устойчивость в точке ветвления G. Во время скачка арка будет проходить из симметричного состояния G через несимметричные состояния в симметричное состояние Н.
Эта нарушающая симметрию неустойчивость связана с неустойчиво симметричной точкой бифуркации G, которая представляет пример неустойчивой сборки. Нарушение симметрии может, конечно, быть вызвано малым несимметричным возмущением или дефектом, которые определят, будет ли при движении стержня положительным или отрицательным (рисунок 1.44).
Рисунок 1.44 - Несимметричная деформация не пологой арки с концами, соединенными пружиной
Аналогичное поведение арки с заделанными концами (которая может рассматриваться как арка с бесконечно жесткой пружиной) показано на рисунке, где отклонение нагрузки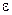 
моделирует начальный дефект. Справа внизу на рисунке показана чувствительность к несовершенствам на графике зависимости несущей способности 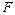от величины 
.
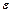Рисунок 1.45 - График зависимости нагрузки от перемещений
и график чувствительности к несовершенствам критической нагрузки для непологой арки с закрепленными концами
