Термин стержень употребляется для перевода нескольких различных английских слов: column, strut, beam, rod, поскольку им соответствует одна и та же математическая модель. Предположим, что мы заострили концы гибкой полоски длиной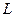 
изготовленной из упругого металла или дерева, и сжимаем ее вдоль оси, используя нагружающее устройство, показанное на рисунке 1.33. Увеличивая медленно нагрузку 
, можно измерить отклонение центральной точки 
и изобразить зависимость от в виде графика. Вместо такого нагружения можно, конечно, использовать червячную передачу, чтобы фиксировать уменьшение длины стержня. Равновесные состояния тогда будут теми же самыми, однако область устойчивости изменится.
Рисунок 1.33 - Поведение сжатого стержня Эйлера (теория и эксперимент)
При нагружении стержня нагрузкой очень малые значения будут регистрироваться до тех пор, пока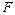 
не приблизится к некоторому критическому значению 
. Как показывают наблюдения, вблизи этой нагрузки боковые отклонения быстро растут с ростом нагрузки. На рисунке зависимость от изображена кривой OKN.
Возрастание , связанное с потерей устойчивости, в дальнейшем замедляется в связи с увеличением жесткости системы в состоянии превышающим критическое. В точке N стержень находится в сильно изогнутом положении, подобном положению, в котором оказывается человек, опершийся на тростник. Несмотря на быстрый рост перемещения около точки , естественная траектория равновесия OKN везде устойчива, и движение вдоль нее гладко и обратимо (что отмечено стрелками на рисунке).
Говоря это, мы подразумевали, что разрушения материала не происходит и необратимых деформаций не возникает, так что поведение материала является упругим и стержень восстанавливает исходную прямую форму при снятии нагрузки.
Стержень может быть сильно изогнут в любом направлении, как с положительным, так и отрицательным значением . При высокой сжимающей нагрузке его можно привести во второе устойчивое состояние М, подталкивая в случае необходимости рукой.
Если затем разгружать стержень, то окажется, что в точке минимума J стержень перепрыгнет обратно в состояние К на естественной траектории нагрузки, при этом во время быстрого динамического хлопка не возникает изменения нагрузки. Последующие нагружение и разгрузка приведут к первоначально наблюдавшемуся гладкому естественному поведению. Скачок в предельной точке J представляет собой пример катастрофы складки.
Допустим, что мы хотим теперь смоделировать это поведение математически. Можно попытаться использовать простую инженерную теорию изгиба, в которой кривизна малого элемента стержня аппроксимируется величиной 
.
При этом 
– перемещение поперечного сечения, находящегося на расстоянии 
от нижней опоры в момент времени 
. Полагая, что кривизна пропорциональна изгибающему моменту, вычисленному в недеформированном состоянии (соответствующему нулевым перемещениям), найдем решение 
.
Это, конечно, правильный ответ для состояния равновесия идеально прямого стержня, однако он ничего не говорит нам об ожидаемой потере устойчивости.
Сжатие прямого упругого стержня понижает собственную частоту до тех пор, пока она, не станет равной нулю. Это происходит при значении нагрузки, равной критическому значению . Анализ линейных колебаний, в котором сохраняются только квадратичные члены энергии, показывает, что корень из основной собственной частоты для первой гармоники 
уменьшается до нуля по линейному закону при увеличении нагрузки до эйлеровой нагрузки потери устойчивости
.
Здесь 
– изгибная жесткость, которая представляет собой произведение модуля Юнга упругости материала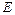 
на момент инерции поперечного сечения 
.
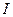Эта критическая нагрузка, которая имеет фундаментальное значение в механике, может быть получена при помощи анализа потери устойчивости в рамках статики, если аппроксимировать кривизну по-прежнему выражением , но изгибающий момент в деформированном состоянии определить как 
. Результат такого линейного анализа соответствующей задачи на собственные значения предсказывает, что перемещение будет стремиться к бесконечности на некотором множестве критических нагрузок, соответствующих гармоническим перемещениям 
, где 
, причем наименьшая критическая нагрузка соответствует 
.
Полный нелинейный статический анализ закритического поведения, использующий более сложное точное выражение для кривизны, дает полную картину равновесия идеального стержня, которая была впервые найдена Эйлером (рисунок 1.34). Фрагмент этой картины для значений нагрузки, близких к 
, показан жирными линиями. Сплошными кривыми обозначаются устойчивые траектории деформации, а штрихами неустойчивые.
Чтобы добиться согласования с экспериментом, надо ввести в математическую модель наличия несовершенств, имеющиеся в стержне, такие, как, начальные отклонения его от прямолинейной формы. Эти несовершенства измеряют основное тривиальное решение, и траектория равновесия уже не проходит через точку бифуркации как показано на полной бифуркационной диаграмме. Здесь светлыми линиями представлены траектории равновесия двух систем, содержащих несовершенства, одна с положительным значением параметра несовершенства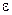 
, другая с отрицательным значением .
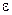Рисунок 1.34 - Трехмерная картина траекторий равновесия
стержня в задаче Эйлера
По-прежнему сплошными и штриховыми кривыми показаны устойчивые и неустойчивые траектории соответственно.
Изобразим поверхность равновесия в трехмерном пространстве обобщенных координат – переменной состояния и двух управляющих параметров и 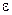. Видно, что устойчиво симметричная точка бифуркации стержня является катастрофой сборки.
