Проанализируем поведение машины Зимана для тех конкретных размеров, которые были указаны выше. Изменение размеров не внесет серьезных качественных отличий в поведение, – факт, в котором в зародыше содержится важная идея, развиваемая нами в полной мере позднее.
Первый шаг состоит в том, чтобы определить положение точки острия Р. В силу соображений симметрии эта точка лежит на оси (рисунок 1.26). Возьмем в качестве единицы длины диаметр диска, так что длины нерастянутых резинок равны 1, а расстояние ОА равно 2.
Снова по симметрии ясно, что когда точка В перемещается вдоль оси, всегда имеется положение равновесия, отвечающее 
.
Точка Р находится там, где равновесие меняется с устойчивого (локальный минимум энергии) на неустойчивое (локальный максимум).
Пусть 
и 
обозначают длины наших двух резинок в положении, когда диск повернут на угол 
, близкий к нулю, но необязательно равный нулю. По закону Гука энергия системы равна
,
где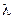 
– модуль упругости резинок.
Рисунок 1.26 - К анализу работы машина Зимана
Далее,
,
и, беря разложение в ряд Тейлора, мы найдем, что
где 
обозначает функцию порядка 4.
Упрощая, получаем
(мы включили члены с 
в ). Следовательно,
.
Аналогично
.
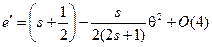Значит,
.
Мы можем пренебречь членом , если коэффициент при 
отличен от нуля. Но коэффициент при в нашем случае
положителен, если 
,
отрицателен, если .
Изменение от минимума энергии к максимуму наблюдается там, где
или
.
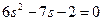Решения этого уравнения таковы:
ясно, что точка Р отвечает положительному значению 
, т. е.
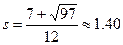
Аналогичное рассуждение с заменой на 
позволяет определить положение верхнего клюва Р', для которого получаем
Можно определить и положение двух боковых клювов, но анализ в этом случае сложнее.
Проведем анализ поведения колеса вблизи точки Р. Член в энергии исчезает в точке Р.
В силу симметрии член с 
также отсутствует, так что мы должны обратиться к члену с . Далее мы работаем с рисунком б.
Пусть свободный конец В находится в точке 
относительно указанной на рисунке системы координат (оси взяты с направлениями, противоположными обычным, из соображений алгебраического удобства).
Формула для получается та же, что и раньше, только теперь мы работаем с точностью до 
и сохраняем члены с , а для имеем формулу
.
Беря разложение соответствующей функции энергии 
с точностью до членов пятого порядка, получаем выражение вида
.
Здесь 
– некоторые константы, точное значение которых не имеет большого значения; приблизительно они равны
, 
, 
, 
, 
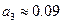В точке Р, где 
, мы имеем функцию вида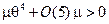 
. При получении качественных результатов для точки Р мы можем пренебречь членом .
Мы можем упростить выражение для функции энергии, отбросив член . Дальнейшие упрощения достигаются таким выбором единиц для физических величин, чтобы 
, устранением кубического члена при помощи замены
;
введением вместо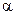 
и 
их подходящих скалярных кратных 
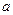и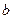 
соответственно (численно они оказываются равными примерно 
и 
). Это приводит к следующему выражению для энергии: 
с некоторой постоянной с.
Так как нас интересуют только критические точки 
, мы можем без потери общности взять 
(или перенести начало отсчета значений энергии). В результате приходим к выражению вида
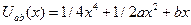
Этой формулой определяется то, что позже мы назовем катастрофой сборки.
Наш следующий шаг, на котором фактически и будет получена полезная информация, состоит в анализе критических точек .
