Дополним этот короткий аналитический экскурс в теорию устойчивости многомодовым линейным гармоническим анализом шарнирно опертого стержня, который взаимодействует (или не взаимодействует) с упругим основанием. Упругое основание действует поперек оси стержня и может быть реализовано как пружинящая подложка, на которой горизонтально лежит стержень. Упругое основание можно представлять себе как большое число упругих пружин, сопротивляющихся поперечным перемещениям 
.
Линеаризованное выражение для энергии, которое требуется в теории колебаний с малой амплитудой и для анализа устойчивости упругого стержня, следует из приведенных выше формул. Энергия деформации изгиба есть
,
потенциальная энергия мертвой осевой сжимающей нагрузки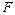 
есть
,
а энергию деформации простого упругого основания, на котором находится стержень, можно записать в виде
,
где 
– жесткость основания. Итак, общая потенциальная энергия 
может быть записана в форме
.
Кинетическая энергия дается равенством
.
Уравнение колебания стержня имеет вид
.
Можно показать, что в случае дискретной модели уравнение для малых колебаний стержня имеет вид
.
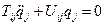И для диагональных коэффициентов энергии имеем
.
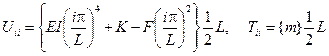Поэтому угловая частота для 
-й моды дается равенством
.
Величины 
суть собственные частоты колебаний шарнирно опертого упругого стержня с массой на единицу длины 
и изгибной жесткостью 
, покоящегося на упругом основании жесткости и несущего осевую сжимающую нагрузку 
. Если положить равными нулю (или, что эквивалентно, 
равными нулю), то получатся критические нагрузки потери устойчивости системы
.
Критические нагрузки для шарнирно опертого стержня, не взаимодействующего с основанием, соответствуют нулевому значению
.
Наименьшая из этих критических нагрузок есть
.
Видно, что для стержня на основании с жесткостью первая гармоника (
) не всегда соответствует наименьшей нагрузке потери устойчивости, как показано на рисунке. По оси ординат отложена приведенная нагрузка 
, а по оси абцис приведенная жесткость 
.
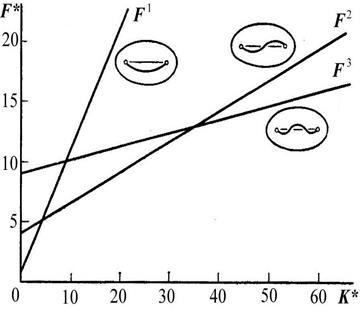
Рисунок 1.41 - Критические нагрузки для стержня на упругом основании в зависимости от меры жесткости основания
Если положить жесткость основания и изгибную жесткость равными нулю (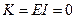
) и написать 
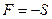, то получим формулу для собственной частоты колебаний струны, растягиваемой усилием 
:
.
