Заголовок этого параграфа может ввести в заблуждение: мы рассматриваем здесь на самом деле статику машины – положения равновесия. Полное ее динамическое описание (что произойдет, если мы крутанем колесо, дернем за резинки нити и т. п.) выходит за рамки рассмотрении, проводимых в этой книге, и принадлежит полнокровной теории динамических систем. Мы займемся тем, что иногда называют квазистатикой: что происходит с положениями равновесия при плавном изменении положения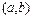 
свободного конца резинки?
Экспериментально этому отвечает очень медленная динамика. Дело в том, что машина быстро успокаивается из-за внутреннего трения в резине. Фактически в слишком аккуратно изготовленной машине с ничтожным трением исследуемые нами эффекты почти полностью маскируются колебаниями. Трение же в оси также маскирует их, доставляя колесу новые положения равновесия, в которых упругие силы не уравновешены.
Теперь, после проведенного выше анализа, мы можем следующим образом рассмотреть изменение положения равновесия с изменением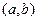 
. Пусть 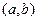проходит некоторый путь в С. Тогда наблюдаемое положение равновесия пройдет путь в 
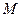, лежащий над путем в С. Из-за складок поверхности 
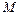этому пути, возможно, придется прыгать с одного листа поверхности на другой. Мы предполагаем, что наша (непрерывная) физическая система делает соответствующие прыжки настолько быстро, что можно пренебречь затрачиваемым на это временем. Исследование положений равновесии само по себе не может сказать нам, где будут происходить прыжки, так как в принципе они возможны в любой точке 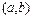, над которой лежит два или больше положений равновесия. Необходимая дополнительная информация содержится в деталях динамики. Однако вместо того чтобы призывать на помощь динамику, мы примем следующее соглашение, которое находится в неплохом соответствии с фактами и которое Том называет принципом (максимального) промедления: система делает прыжок лишь тогда, когда у нее не остается другого выбора. Это означает, что путь, проходимый положением равновесия, сменяет лист на поверхности, лишь когда он проходит через складку, и лист, на котором он находился, исчезает. Для быстрых изменений управляющих параметров этот принцип нарушается.
Рисунок 1.30 - Работа машины Зимана, когнда путь входит в область с снизу слева и выходит из нее снизу справа
Поскольку проведенный нами анализ относится к положениям равновесия вблизи точки 
, мы можем ответить на заданный ранее вопрос, для случая, когда путь входит в область с снизу слева и выходит из нее снизу справа. Такой путь в С вместе с соответствующим путем положения равновесия, получаемым по принципу промедления, показан на рисунке. Из него видно, что прыжок происходит, когда путь покидает область, но не когда он в нее входит. Последовательность графиков для функций энергии 
и соответствующие критические точки показаны на рисунке: прыжок происходит, когда минимум и максимум сливаются и уничтожают друг друга.
Рисунок 1.31 - Возможные критические точки для машины Зимана
Прыжки являются примерами того, что Том и Зиман называют катастрофическими прыжками (скачками). Ниже мы будем называть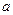 
и 
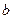переменными управления (или управляющими переменными, или управляющими параметрами), a 
– переменной поведения (или переменной состояния, или поведенческой переменной).
При помощи катастрофы сборки Уитни объясняются, следующие явления, которые экспериментально проверяются на машине.
Первое явление – катастрофические прыжки происходят тогда, когда гладкие изменения в управлении вызывают разрывные изменения состояния.
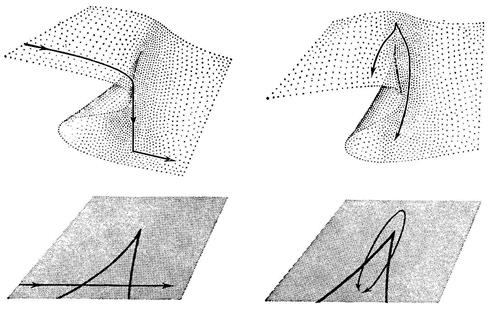
Второе явление – гистерезис (название взято по аналогии с подобным явлением в магнетизме, которое, по всей видимости, может быть подведено под рассматриваемую теорию). Если мы обратим путь в плоскости параметров, это не обязательно приведет к обращению пути в пространстве состояний. Это продемонстрировано на рисунке а. Принцип промедления снова показывает, что прыжок происходит при прохождении бифуркационного множества, но так как мы теперь путешествуем в обратную сторону, это произойдет на другой стороне области.
Третье явление – расхождение: небольшие различия в пути могут повлечь за собой (без всяких скачков) большие различия в состоянии, даже если пути начинаются и кончаются в одних и тех же точках (рисунке 1.31 б).
Четвертое заключается в том, что из одного состояния в другое можно перейти или гладко, или со скачком, в зависимости от пути (рисунке 1.31 в). Можно было бы отметить и многие другие явления. Мы будем дальше исследовать их по мере необходимости. Читателю стоит проверить, что отмеченные четыре явления действительно имеют место в нашей машине.
Используя принцип промедления, читатель может теперь с помощью этой поверхности предсказать поведение машины для любых путей, которые различными способами обходят клювы, и притом без всякого труда; сомнительно, смог ли бы он это сделать, не имея перед собой рисунок.
А б
В
Рисунок 1.31 - При помощи катастрофы сборки объясняются, следующие явления: а – гистерезис; б – расхождение;
в – возможность различных путей (со качком и без него)
