Поскольку при одноступенчатом контроле решение принимают по результатам проверки только одной выборки или пробы, эта выборка должна хорошо отражать свойства всей партии и для этого быть случайной. Случайную выборку получают отбором единиц продукции из различных частей партии или перемешиванием единиц продукции в партии при отборе.
Планом одноступенчатого контроля устанавливается объем выборки n из партии объемом N а приемочное число с. Партия принимается, если количество дефектных единиц продукции в выборке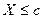 
; при 
партия бракуется.
Процедуру одноступенчатого контроля наглядно отображает схема (рис. 3.9), из которой по горизонтальной оси отложено количество проверяемых единиц Продукции, по вертикальной - количество забракованных единиц продукции. Для каждой выборки эти крестики располагаются по случайному пути, который закапчивается в точке с абсциссой n. Партия принимается или бракуется в зависимости от того, попадает ли точка окончания случайного пути ниже или выше с.
При одноступенчатом контроле партия принимается, если наступает одно из несовместных событий: 
, 
,…, 
. По-этому вероятность приемки партии равна сумме вероятностен этих событий:
(3.13)
Слагаемые в формуле (3.13) зависят от вида закона распределения случайной величины 
— количества дефектных единиц продукции в выборке из n единиц продукции.
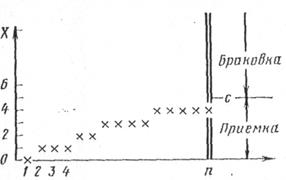
Рис 3.9 Схема одноступенчатого приемочного контроля.
Для малых партий, когда объем выборки превышает 10...25% партии (наиболее сложный случай), можно использовать гипергеометрическое распределение:
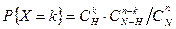, (3.14)
где k = 0, 1, 2,...; 
- целое число.
При таком распределении учитывается зависимость результатов отдельных испытаний от изменения объема малой партии при взятии из нее выборки, поэтому обеспечивается хорошее приближение к действительности. Однако это распределение имеет три параметра (
, 
, 
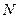), поэтому трудно составлять таблицы и пользоваться ими. Чаще применяют биномиальное распределение, согласно которому
(3.15)
Это распределение имеет два параметра (
, ) и поэтому пользоваться таблицами удобно.
Биномиальное распределение соответствует случаю, когда испытания отдельных изделии независимы, что можно достичь возвращением проверенных изделии в партию. Испытания считаются практически независимыми при 
, что обычно и бывает в действительности. Поэтому биномиальное распределение применяют чаще гипергеометрического.
Когда, не только , но и q мало (т. е. 
- мало дефектных единиц продукции в партии), можно использовать распределение Пуассона с параметром 
:
(3.16)
Этим распределением пользоваться еще проще, так как оно имеет одни параметр.
Подставив в форму (3.13) одно из выражении для 
согласно (3.14), (3.15) или (3.16), получим зависимость 
.
Согласно определениям вероятностей ошибок первого и второго рода имеем
, (3.17)
. (3.18)
В (3.17) учтено, что так как 
- вероятность забракования партии продукции; обладающей приемочным уровнем дефектности 
, то 
- вероятность приемки этой партии.
По формулам (3.17) и (3.18) можно вычислить и 
по выбранным заранее , 
, , 
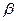при определенном виде закона распределения . Например, для распределения Пуассона:
; (3.19)
. (3.20)
Решение уравнений (3.19), (3.20) в явном виде обычно получить трудно. Приходится так изменять и , чтобы суммы были равны правым частям уравнений.
Для построения оперативной характеристики обычно достаточно четырех точек: 
; 
и значении из уравнении (3.19) и (3.20).
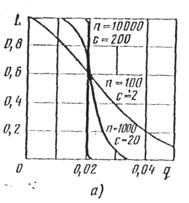
Влияние на оперативную характеристику объема выборки и приемочного числа показано на рис. 3.10. Если увеличивать при неизменном отношении 
, то оперативная характеристика становится все ближе к идеальной (рис. 3.10, а). При этом соответственно увеличивается стоимость контроля.
| 
| 
|
Рис. 3.10. Влияние объема выборки и приемочного числа на оперативную характеристику одноступенчатого плана контроля (биномиальное распределение):
а)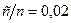 
; б) 
; в) 
.
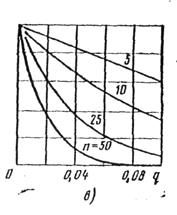
Увеличение приемочного числа при неизменном объеме выборки смещает 
вправо и уменьшает ее наклон в рабочей области (, ). При оперативная характеристика близка к экспоненте. Если задаться определенной вероятностью (
) приемки, то на рис. 3.10, б видно, что при обеспечивается приемка при минимальной доле дефектных единиц продукции. Поэтому условие применяют при контроле изделий, к качеству которых предъявляются высокие требования.
Увеличение при постоянном приемочном числе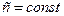 
ведет к смещению влево (рис. 3.10, в).
