Анализ поведения случайных траекторий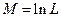 
показывает, что моменты окончания испытаний являются случайными величинами (см. рис. 3.8).
Рис. 3.8
Причем в случае приемки партии выполняется соотношение
,
В этом случае вероятность приемки правильной гипотезы равна 
Соответственно, если произойдет браковка, то
,
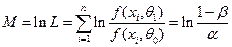При этом вероятность браковки правильной гипотезы равна 
.
Можно доказать, что
.
С другой стороны матеиатическое ожидание можно оценить по соотношению (см. рис. 3.8)
Отсюда
,
где 
Таким образом
В дальнейшем найдем средние объемы испытаний для различных законах распределения параметров раьотоспособности системы:
А) Планирование испытаний при биномиальном законе распределения
В этом случае математическое ожидание логарифма отношения значений плотности распределения случайной величины x при 
и 
определяется по известному выражению
.
Тогда средний объем испытаний, необходимый для подтверждения заданного показателя надежности 
, находится по формуле (
).
.
Б) Планирование испытаний в случае, если параметр подчиняется нормальному закону
Найдем математическое ожидание логарифма отношения значений функции плотности распределения 
наработки на отказ при 
и 
.
Обозначим
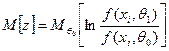(3.11)
или 
,
где 
.
Принимая 
, находим отношение правдоподобия
(3.12).
Подставляя выражение (3.12) в (3.11) и интегрируя, найдем
Средний объем испытаний, необходимый для подтверждения заданного показателя надежности, определяется по формуле ()
.
В) Планирование испытаний в случае, если параметр подчиняется экспоненциальному закону
Для определения среднего объёма испытаний найдем математическое ожидание логарифма отношения значений функций плотности распределения наработки на отказ 
при 
и 
.
Проинтегрировав выражение, получим
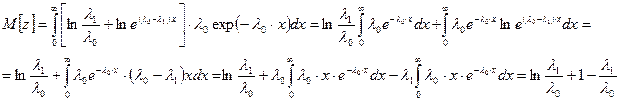
В этом случае средний объем испытаний, необходимый для подтверждения заданного показателя, определяется по формуле ()
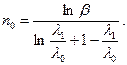
Для сравнения полученных объёмов испытании при нормальном законе распределения классическим методом и методом последовательного анализа с односторонней границей найдем отношение этих объемов и определим средний выигрыш.
Найдем отношение объемов испытаний по формуле
,
где 
- последовательный анализ; 
- метод Неймана.
Так как при планировании испытаний последние не бракуются, то риск поставщика равен нулю ().
При квантиль 
.
Окончательно можно написать
Как видно из равенства отношение объемов испытаний зависит лишь от риска заказчика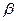 
и не зависит от показателя надежности. Средний выигрыш в объеме испытаний методом последовательного анализа с односторонней границей по сравнению с классическим методом в относительных единицах для различных значений 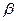приведен в табл. 3.3
Таблица 3.3
| Риск заказчика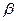
| 
| 
| 
| 
|
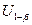
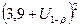
| 0,25 | 0,674 | -2,763 | 20,92 | 0,13 |
| 0,20 | 0,842 | -3,218 | 22,48 | 0,14 |
| 0,15 | 1,036 | -3,794 | 24,36 | 0,15 |
| 0,10 | 1,282 | -4,605 | 26,85 | 0,17 |
| 0,05 | 1,645 | -5,991 | 30,74 | 0,19 |
| 0,01 | 2,326 | -9,210 | 38,76 | 0,24 |
| 0,005 | 2,576 | -10,596 | 41,94 | 0,25 |
| 0,001 | 3,09 | -13,815 | 48,86 | 0,28 |
Анализ табл. свидетельствует о том, что с уменьшением риска заказчика уменьшается и выигрыш в объеме испытаний. Так как для изделий военного назначения риск заказчика обычно принимается в пределах от 0,1 до 0,01, то в среднем объем при планировании испытаний методом последовательного анализа с односторонней границей Для нормального закона существенно уменьшается по сравнению с методом фиксированного объема.
