Последовательный анализ появился в 1942 – 1943 гг. в связи с поиском более эффективных, чем классические, методов статистического приемочного контроля массовой продукции промышленности. Создателем этого метода является американский статистик А. Вальд.
Рассмотрим применение последовательного анализа к задаче различия гипотез 
и 
. Предложим, что гипотезы относятся к параметру Q, т. е. 
, 
. Требуется найти выборочную схему, делящую выборочное пространство на три взаимно непересекающиеся области:
а) 
, при попадании в которую выборочной точки принимается гипотеза ;
б) 
, при попадании в которую выборочной точки принимается гипотеза ;
в) 
— остальная часть выборочного пространства, при попадании в которую выборочной точки выбор продолжается.
Поставленная задача состоит в построения функция 
, называемой решающей функцией (или решающим правилом), которая каждой выборочной точке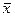 
ставит в соответствие некоторый элемент 
так, что при наблюдении 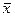выносится решение . Согласно критерию отношения вероятностей Вальда, последовательное решающее правило состоит в следующем.
Строится отношение правдоподобия:
(3.9)
Отметим, что 
- это условная плотность вероятности для наблюдаемых значений 
при истинности гипотезы 
(
).
В дальнейшем величина 
сравнивается с постоянными порогом А и В. Если 
, то принимается гипотеза ; если 
, то принимается гипотеза , если 
, то делается еще одно наблюдение (выбор продолжается). После логарифмирования критическое неравенство примет вид
Рассмотренный критерий называется последовательным критерием отношения вероятностей. Очевидно, последовательный критерий отношения вероятностей обладает определенными оптимальными свойствами, так как он использует всю имеющуюся в распоряжении информацию, включая порядок появления выборочных значений.
Теперь определим значения порогов А и В. Рассмотрим выборку, для которой лежит между А и В для первых 
испытаний, так что принимаем (отвергаем ). Согласно (3.9) вероятность получения такой выборки по крайней мере в А раз больше при гипотезе , чем при гипотезе . Учитывая, что вероятность принятия , когда выполняется , равна 
, а вероятность принятия , когда выполняется , равна 
, можно записать;
.
Отсюда
Аналогично, рассматривая случаи, когда принимается , получим
На практике более удобным является вычисление логарифма отношения правдоподобия, чем непосредственное вычисление отношения правдоподобия.
Тогда неравенства примут вид
- условие продолжения испытаний,
- условие браковки,
- условие приемки.
Соотношение между постоянными А и В выглядит в следующем виде:
, , (3.10)
где - риск поставщика;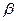 
- риск заказчика.
В дальнейшем рассмотрим построение областей отработки для различных законов рпспределения параметров работоспособности системы:
