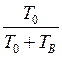Показатели работоспособности восстанавливаемых систем

В системе многократного применения периоды работы, в которые она решает поставленную задачу, чередуются с периодами простоя, в которые происходит восстановление (ремонт). Такая си­стема может находиться в одном из двух состояний: исправном или не­исправном. Поэтому можно написать

 

(4.1)

где Р_и(0) — вероятность того, что система находится в исправном состоянии; Р_в(t)— вероятность того, что система находится в неисправ­ном состоянии (в состоянии восстановления).

Целесообразно считать, что чем больше времени система находит­ся в работоспособном состоянии и чем меньше время вынужденных простоев, тем выше ее состояние к применению — готовность. Для коли­чественной оценки состояния к применению вводят понятия коэффици­ента готовности. Под коэффициентом готовности понимается вероятность того, что в заданный момент времени система исправна, т. е. К_Г(t)=Р_И(t), где Р_И(t) —вероятность нахождения системы в исправном состоянии в момент t. Считается, что коэффициент готовности — это веро­ятность того, что система (или комплекс в целом) окажется работо­способной в произвольный момент времени, кроме планируемых перио­дов, в течение которых использование системы по назначению не преду­сматривается.

Если среднее время безотказной работы аппаратуры и среднее время восстановления (ремонта) распределены по экспоненциальному закону, то уравнение для коэффициента готовности К_Г(t) выражается формулой

(4.2)

 

В соответствии с (4.2) вероятность нахождения системы в работоспо­собном состоянии зависит от безотказности работы Т₀, восстанавливае­мости Т_в и времени эксплуатации t. В пределе, когда t→∞, приходим к выражению

 

Таким образом, в установившемся (стационарном) процессе эксплуа­тации коэффициент готовности не зависит от состояния системы в на­чале ее эксплуатации. График зависимости К_Г(t) показан на рис. 4.1

 

KГ(t)

t

 

Рис. 4.1 Зависимость K_Г(t).

 

Для современных систем дли­тельного использования всегда выполняется условие Т₀>Т_В. Тогда можно записать

Следовательно, коэффициент готов­ности показывает относительное вре­мя нахождения системы в исправ­ном состоянии (в состоянии готовно­сти к применению) в установившем­ся (стационарном) процессе эксплуатации. Величина К_Г может быть повышена как за счет увеличения наработки на отказ, так и за счет сокращения среднего времени вос­становления.

Для практического расчета коэффициента готовности можно вос­пользоваться формулой

(4.3)

где t_i — время нахождения системы в исправном состоянии между (i —1) - м и i - м отказом; t_Bi — время, затрачиваемое на восстановление системы после возникновения i-го отказа; n — число отказов за рассма­триваемый период эксплуатации.

Статистически коэффициент готовности определяется отношением суммарного времени пребывания наблюдаемых систем в работоспособ­ном состоянии к произведению числа этих систем на продолжительность эксплуатации (за исключением простоев на проведение плановых ремонтов и технического обслуживания)

где t_ip — суммарное время пребывания i-й системы в работоспособном состоянии (i=1,2,...,); Т_РВ — продолжительность эксплуатации, со­стоящей из последовательно чередующихся интервалов времени рабо­ты и восстановления.

Пример: РТС работала по 8 ч. Ежедневно в течение 30 дней. Определить коэффициент готовности, если за это время было два отказа, на устра-

нение которых затрачено в общей сложности 5 ч. Решение: В соответствии с (4.3) получим КГ = 30*8/(240+5) = 0,98

Коэффициент простоя. Если система в произвольный момент не­исправна, значит, она восстанавливается (находится в состоянии про­стоя).

Математическое выражение для расчета вероятности нахождения системы в состоянии восстановления (простоя) определится, если в (3.1) подставить значение Р_И(t) = K_Г(t) из (3.2). Тогда получим

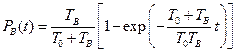(4.4)

 

При Т₀ >> Т_В вероятность Р_В(t) быстро стремится к своему стацио­нарному значению. Стационарное значение этой вероятности опреде­ляется путем перехода к пределу

Это стационарное значение вероятности нахождения системы в со­стоянии простоя называется коэффициентом простоя

(4.5)

Коэффициенты простоя и готовности связаны соотношением

(4.6)

Расчетные формулы для определения коэффициента простоя

 

 

где - суммарное время пребывания i-го объекта в состоянии про­стоя (i=1,2,...,m).

Если известен один из коэффициентов К_Г или К_ВП, то второй вычисляется по формуле (4.6).

Следует указать на ту особенность, что коэффициент готовности не учитывает простои системы при техническом обслуживании (ТО). Поэтому он используется для оценки систем, которые работают не непрерывно, а по сеансам (расписанию). Техническое обслуживание та­кой системы может выполняться в интервалах между применениями. Этого нельзя сделать на системах, работающих непрерывно. В общем случае система может находиться в различных состояниях: работы, восстановления после отказа, техническом обслуживании, и т.д. Для оценки этих состояний, кроме коэффициента готовности рассматривается также коэффициент технического использования.

Коэффициент технического использования— это отношение математического ожидания времени пребывания системы в работоспособном состоянии за некоторый период эксплуатации к сумме математических ожиданий времени пребывания системы в работоспособном состоянии, времени простоев, обусловленных техническим обслуживанием, и времени ремонтов за тот же период эксплуатации. Статистически определяется по соотношению

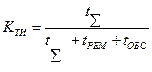(4.7)

где 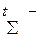суммарная наработка системы; 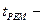суммарное время простоев из-за ремонтов; 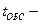суммарное время простоев из-за планового технического обслуживания..

 

 

При решении практических задач иногда используется так называемый коэффициент оперативной готовности. Нестационарный коэффициент оперативной готовности характеризует вероятность того, что исправная к моменту t система не откажет на следующем интервале времени (t, t+x). Если положить x=0, то для этого частного случая мы приходим к нестационарному коэффициенту готовности. При приходим к стационарному коэффициенту оперативной готовности 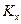. Можно доказать справедливость следующего соотношения

, (4.8)

где среднее время безотказной работы системы; среднее время восстановления;

P(t) – вероятность безотказной работы системы.

Для экспоненциального распределения наработки до отказа соотношение примет вид

.

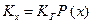В общем случае, для систем стареющего типа, справедлива следующая оценка

(4.9)