Для определения критической области статистики используют уровень значимости 
и учитывают вид альтернативной гипотезы 
. Основная гипотеза 
о значении неизвестного параметра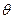 
распределения выглядит так:
.
Альтернативная гипотеза может при этом иметь следующий вид:
, 
или 
Соответственно можно получить левостороннюю, правостороннюю или двустороннюю критические области.
Проверка статистической гипотезы состоит из следующих этапов:
1) определение гипотез и ;
2) выбор статистики и задание уровня значимости ;
3) определение по таблицам, по уровню значимости и по альтернативной гипотезе критической области;
4) вычисление по выборке значения статистики;
5) сравнение значений статистики с критической областью;
6) принятие решения: если значение статистики не входит в критическую область, то принимается гипотеза и отвергается гипотеза , а если входит в критическую область, то отвергается гипотеза и принимается гипотеза .
7) приемочный уровень 
и число испытаний 
определяются из решения системы:
.
В дальнейшем предположим, что случайная величина Х распределена нормально.
Ставится задача различения двух гипотез о значении математического ожидания:
Для заданного риска поставщика, имеем
;
где -- приемочный уровень, 
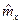-- точечная оценка математического ожидания.
Отсюда
;
где -- обьем выборки, 
-- среднее квадратическое отклонение.
Приравнивая аргументы,получим
.
Принимая риск заказчика,равным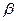 
,найдем
;
Отсюда
;
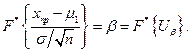Приравнивая аргументы, получим
.
Вычитая из первого раваенства второе, найдем
;
Отсюда
(3.7)
Из первого соотношения имеем
Отсюда
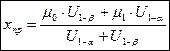(3.8)
