Включение: пусть Е – множество, М – множество принадлежностей, А и В – два нечетких подмножества множества Е. Будем говорить, что А содержится в В, если 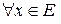 m B (x) ³ m A (x), и обозначать эту операцию А ÌÌ В.
m B (x) ³ m A (x), и обозначать эту операцию А ÌÌ В.
Пример 1.6. Пусть Е = { x 1, x 2, x 3, x 4}, 0 ≤ M ≤ 1,
А = {(x 1|0,4), (x 2|0,2), (x 3|0), (x 4|1)},
B = {(x 1|0,3), (x 2|0), (x 3|0), (x 4|0)}.
В соответствии с определением В ÌÌ А.
Равенство: пусть Е – множество, М – множество принадлежностей, А и В – два нечетких подмножества множества Е. Будем говорить, что А и В равны тогда и только тогда, когда 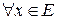 m B (x) = m A (x).
m B (x) = m A (x).
Пример 1.7. Пусть Е = { x 1, x 2, x 3, x 4}, 0 ≤ M ≤ 1,
А = {(x 1|0,4), (x 2|0,2), (x 3|0), (x 4|1)},
B = {(x 1|0,4), (x 2|0,2), (x 3|0), (x 4|1)}.
В соответствии с определением В = А.
Дополнение: пусть Е – множество, М – множество принадлежностей, А и В – два нечетких подмножества множества Е. Скажем, что А и В дополняют друг друга, если  m B (x) = 1 – m A (x).
m B (x) = 1 – m A (x).
Пример 1.8. Пусть Е = { x 1, x 2, x 3, x 4}, 0 ≤ M ≤ 1,
А = {(x 1|0,4), (x 2|0,2), (x 3|0), (x 4|1)},
B = {(x 1|0,6), (x 2|0,8), (x 3|1), (x 4|0)}.
В соответствии с определением В = 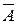 или А =
или А = 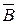 .
.
Пересечение: пусть Е – множество, М – множество принадлежностей, А и В – два нечетких подмножества множества Е. Пересечение А Ç В определяют как наибольшее нечеткое подмножество, содержащееся одновременно в А и В:
 m А Ç В (x) = min(m A (x), (m В (x)). (1.35)
m А Ç В (x) = min(m A (x), (m В (x)). (1.35)
Пример 1.9. Пусть Е = { x 1, x 2, x 3, x 4, x 5}, 0 ≤ M ≤ 1,
А = {(x 1|0,2), (x 2|0,7), (x 3|1), (x 4|0)), (x 5|0,5)},
B = {(x 1|0,5), (x 2|0,3), (x 3|1), (x 4|0,1), (x 5|0,5)}.
Тогда А Ç В = {(x 1|0,2), (x 2|0,3), (x 3|1), (x 4|0), (x 5|0,5)}.
На основе (1.35) можно записать 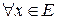
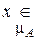 А и
А и 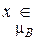 В => =>
В => => 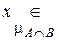 А Ç В. Это позволяет ввести понятие «нечеткое и» – И.
А Ç В. Это позволяет ввести понятие «нечеткое и» – И.
Пример 1.10. Если А – нечеткое подмножество действительных чисел, очень близких к 5, и В – нечеткое подмножество действительных чисел, очень близких к 10,
А = {(9|0,2), (6|0,8), (5|1), (10|0,1)), (7,5|0,5)},
B = {(9|0,8), (6|0,2), (5|0,1), (10|1), (7,5|0,5)},
то А Ç В – нечеткое подмножество действительных числе, очень близких к 5 И 10.
Тогда А Ç В = {(9|0,2), (6|0,2), (5|0,1), (10|0,1), (7,5|0,5)}.
Эту операцию можно проиллюстрировать на рис. 1.3, где А Ç В –заштрихованная взаимопересекающаяся часть двух окружностей вокруг точек 5 и 10.

Рис. 1.3. Графическая иллюстрация
операции пересечения двух нечетких множеств
Объединение: пусть Е – множество, М – множество принадлежностей, А и В – два нечетких подмножества множества Е. Объединение А È В определяют как наименьшее нечеткое подмножество, которое содержит как А, так и В:
 m А È В (x) = max(m A (x), (m В (x)). (1.36)
m А È В (x) = max(m A (x), (m В (x)). (1.36)
Пример 1.11. Пусть Е = { x 1, x 2, x 3, x 4, x 5}, 0 ≤ M ≤ 1,
А = {(x 1|0,2), (x 2|0,7), (x 3|1), (x 4|0), (x 5|0,5)},
B = {(x 1|0,5), (x 2|0,3), (x 3|1), (x 4|0,1), (x 5|0,5)},
тогда А È В = {(x 1|0,5), (x 2|0,7), (x 3|1), (x 4|0,1), (x 5|0,5)}.
На основе (1.36) можно записать 
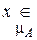 А или
А или 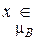 В =>
В =>  А È В. Это позволяет ввести понятие «нечеткое или» – ИЛИ.
А È В. Это позволяет ввести понятие «нечеткое или» – ИЛИ.
Пример 1.12. Если А – нечеткое подмножество действительных чисел, очень близких к 5, В – нечеткое подмножество действительных чисел, очень близких к 10,
А = {(9|0,2), (6|0,8), (5|1), (10|0,1)), (7,5|0,5)},
B = {(9|0,8), (6|0,2), (5|0,1), (10|1), (7,5|0,5)},
то А È В – нечеткое подмножество действительных числе, очень близких к 5 ИЛИ 10. Тогда А Ç В = {(9|0,8), (6|0,8), (5|1), (10|1), (7,5|0,5)}.






