Технические системы, их подсистемы и элементы систем могут работать в режиме, когда восстановление со стороны ремонтного персонала возможно, и в режиме, когда это невозможно либо нецелесообразно. Поэтому для восстанавливаемых и для невосстанавливаемых элементов и систем применяются различные показатели надежности и различные методы расчета надежности.
1. Вероятность безотказной работы объекта P (t) выражает вероятность того, что невосстанавливаемый объект не откажет к моменту времени t.
2. Если F (t) – вероятность того, что невосстанавливаемый объект откажет к моменту времени t, то P (t) = 1 – F (t).
P (t) обладает следующими свойствами:
а) P (0) = 1 (предполагается, что до начала работы изделие является безусловно работоспособным);
б) 
(предполагается, что объект не может сохранить свою работоспособность неограниченно долго);
в) если t 2 > t 1, то 
(вероятность безотказной работы –функция невозрастающая).
Статистически определить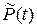 
по результатам испытаний можно с помощью следующей формулы:
, (2.1)
где N (t) – число исправных объектов в момент времени t; N (0)– число исправных объектов в начальный момент времени.
2. Вероятность безотказной работы в интервале времени от t 1 до t 2:
(2.2)
(2.3)
3. Вероятность отказа Q (t) выражает вероятность того, что невосстанавливаемый объект откажет к моменту времени t:
(2.4)
(2.5)
где N (t) – число исправных объектов в момент времени t; n (t) – число отказавших объектов к моменту времени t.
4. Вероятность отказа в интервале времени от t 1 до t 2:
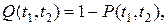(2.6)
(2.7)
5. Плотность распределения отказов f (t) определяет вероятность возникновения отказа в момент времени t:
(2.8)
Статистическая оценка 
производится за интервал времени D t, так как функция f (t) является дифференциальной:
(2.9)
Поэтому можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент из множества всех объектов, поставленных на испытания. В связи с этим f (t) на практике обычно называют частотой отказов.
6. Интенсивность отказов l(t) определяет вероятность возникновения отказа в момент времени t с учетом числа объектов, работоспособных к моменту времени t:
(2.10)
(2.11)
Поэтому 
можно рассматривать как среднее число отказов в единицу времени непосредственно после момента t, приходящееся на один элемент, из всех объектов, продолжающих работать к этому моменту t. Отсюда видно, что l(t) характеризует надежность объекта в момент t, этим и объясняется более широкое применение на практике этого показателя. Поскольку на практике единицы времени достаточно велики (при испытаниях Δ t может достигать нескольких десятков часов), в числителе стоит усредненное число работоспособных изделий на начало и конец интервала времени Δ t.
7. Среднее время наработки на отказ T определяется как математическое ожидание времени до отказа:
(2.12)
. (2.13)
8. Дисперсия наработки до отказа Dt. Средняя наработка до отказа является точечной оценкой и не говорит ничего о характере времени до отказа. Две совершенно различные функции P 1(t) и P 2(t) (рис. 2.1) могут характеризоваться одинаковыми значениями средней наработки на отказ Т 1 = Т 2. Чтобы различать такие случаи, наряду с показателем Т используется показатель Dt – дисперсия наработки до отказа (среднеквадратическое отклонение наработки до отказа – 
):
(2.14)
Рис. 2.1. Пример различных функций
с одинаковым значением наработки на отказ
Дисперсия характеризует величину разброса наработки относительно среднего значения:
(2.15)
где Ti – время отказа i объекта.
Пример 2.1. Пусть на испытания было поставлено 35 объектов. Количество отказавших объектов подсчитывали каждые 2 ч. В результате получился следующий ряд значений:
| ti | ||||||||||
| n (ti) |
Определим 
– интегральную функцию распределения до отказа:
| ti | ||||||||||
| 3/35 | 6/35 | 11/35 | 19/35 | 26/35 | 32/35 | 34/35 | 35/35 | 35/35 |
Вероятность отказа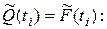 
| ti | ||||||||||
| 0,086 | 0,172 | 0,314 | 0,534 | 0,743 | 0,914 | 0,971 | 1,00 | 1,00 |
Вероятность безотказной работы 
| ti | ||||||||||
| 0,914 | 0,828 | 0,686 | 0,466 | 0,257 | 0,086 | 0,029 |
Вероятность безотказной работы в интервале от 4 до 12 ч:
Вероятность отказа в интервале от 4 до 12 ч:
Плотность распределения отказов 
| ti | ||||||||||
| 
| 
| 
| 
| 
| 
| 
| 
|
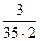
Интенсивность отказов 
| ti | ||||||||||
| 
| 
| 
| 
| 
| 
| 
| 
|
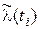
Среднее время наработки на отказ 
:
= (2×3 + 4×3 + 6×5 + 8×8 + 10×7 + 12×6 + 14×2 + 16×1) / 35» 8,52.
Следует обратить внимание, что при расчете среднего времени наработки на отказ число отказавших элементов на данном интервале умножается не на время, соответствующее концу интервала, а на время, соответствующее началу. Действительно, обратившись к исходной таблице, мы видим, что за период с 0 до 2 не отказал ни один элемент. С 2 до 4 ч отказали 3 элемента. Эти три элемента не проработали 4 ч. Все, что мы можем сказать, это то, что они проработали 2 ч и, возможно, еще некоторое время после этого. Поэтому эти три элемента входят в выражение для подсчета среднего времени наработки на отказ с временем работы 2, и, таким образом, оценка получается несколько заниженной.
Дисперсия:
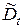= (6,522×3 + 4,522×3 + 2,522×5 + 0,582×8 + 1,482×7 + 3,482×6 + 5,482×2 +
+ 7,482) / 35» 12,193.
.
