Рассматривать понятие принадлежности для нечетких подмножеств начнем с примера. Обратимся к выражению (1.24). В нем, как было отмечено, функция принадлежности m принимает только значения 1 и 0. Представим теперь, что m может принимать любое значения из интервала (0,1). Тогда степени принадлежности элемента xi к нечеткомуподмножеству А могут быть записаны следующим образом:
– xi не принадлежит к А, m А (xi) = 0;
– xi в небольшой степени принадлежит к А, m А (xi) близко к 0;
– xi более или менее принадлежит к А, m А (xi) равноудалена от 0 и 1;
…
– xi принадлежит к А, m А (xi) = 1.
Тогда А = {(x 1|0,2), (x 2|0), (x 3|0,3), (x 4|1), (x 5|0,8)} будет представлять собой нечеткое подмножество множества Е. Будем записывать A Ì E или A Ì E.
Принадлежность элемента к нечеткому подмножеству можно обозначить следующим образом: x1  A, x 2
A, x 2 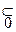 A, x4
A, x4 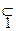 A. Эти обозначения могут быть истолкованы следующим образом:
A. Эти обозначения могут быть истолкованы следующим образом:
– x 2не принадлежит к А (m А (x 2) = 0));
– x 1в небольшой степени принадлежит к А (m А (x 1) = 0,2));
– x 4принадлежит к А (m А (x 4) = 1)).
Возвращаясь к обозначениям теории множеств, можно говорить, что
Î – эквивалентно 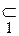 , Ï – эквивалентно
, Ï – эквивалентно 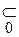 .
.
Определение: Пусть Е – множество, счетное или нет, и х – элемент Е. Тогда нечетким подмножеством А множества Е называется множество упорядоченных пар {(x |m A (x))} " x Î E, где m A (x) – характеристическая функция принадлежности,которая принимает свои значения во вполне упорядоченном множестве М и указывает вероятностьпринадлежности элемента х подмножеству А. Множество М будем называть множеством принадлежностей.
Если М = {0,1}, то нечеткое подмножество А переходит в «обычное» четкое подмножество.
Приведем несколько примеров.
Пример 1.3. Запишем нечеткое подмножество чисел х, приблизительно равных данному действительному числу n, где n Î R (R – множество действительных чисел):
А = {…(n – 1|0,8), (n – 0,5|0,9), (n |1), (n + 0,5|0,9), (n + 1|0,8)…}.
Пример 1.4. Пусть N – множество натуральных чисел,
N = {0, 1, 2, 3, 4, 5, 6…}.
Рассмотрим нечеткое подмножество «небольших» натуральных чисел:
А = {(0|1), (1|0.8), (2|0,6), (3|0,4), (4|0,2), (5|0), (6|0)…}.
Разумеется, m A (x) в этих примерах задается субъективно. Последнее выражение можно переписать в виде
0 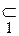 A, 1
A, 1  A, 2
A, 2 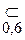 A, 3
A, 3 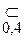 A,….
A,….






