Элементы теории нечетких множеств

Введение элементов теории нечетких множеств в данное учебное по­собие связано с тем, что иногда невозможно заранее получить точные на­дежностные характеристики элементов и блоков разрабатываемой сис­темы. В таких условиях приходится брать несколько надежностных харак­теристик одного элемента, ранжируя их по степени достоверности, и про­водить оптимизацию структуры системы, исходя из определенных крите­риев [3]. Такой подход изложен, в частности, в подразд. 2.5.

1.4.1. Понятие принадлежности и основные операции­ для четких подмножеств

 

Рассмотрим понятие принадлежности сначала на примере четких множеств.

Пусть Е – множество, А – подмножество Е. Имеется также характе­ристическая функция m _А (х), которую в упрощенном варианте будем счи­тать вероятностью того, принадлежит ли элемент x подмножеству А:

 

(1.21)

т.е. вероятность для четких множеств принимает только значения 0 и 1 (принадлежит либо не принадлежит).

Предположим, что множество Е состоит из нескольких элементов:

 

Е = { x ₁, x ₂, x ₃, x ₄, x ₅}, (1.22)

 

а подмножество А – из некоторых элементов множества Е:

 

А = { x ₂, x ₃, x₅}. (1.23)

 

Тогда подмножество А можно записать через элементы множества Е и значения функции m _А (х) (принадлежности элемента подмножеству А).

Пример 1.1. Запишем конкретные значения подмножества А:

 

А = {(х ₁,0), (x ₂,1), (x ₃,1), (х ₄,0), (x ₅,1)}. (1.24)

 

Это означает: элемент x ₁ принадлежит подмножеству А с вероятно­стью m _А (х ₁) = 0, т.е. не принадлежит подмножеству А, в то время как эле­мент x ₂ принадлежит подмножеству А с m _А (х ₂) = 1, т.е. принадлежит под­множе­ству А.

Для четких множеств определены несколько операций. Наиболее часто употребляются:

– дополнение

Ā ≡ { x E || x A },

 

, , (1.25)

или, если записать эти соотношения через характеристическую функцию принадлежности,

 

; (1.26)

 

– пересечение АÇВ или, если определить эту операцию через функ­цию принадлежности,

 

(1.27)

 

,

 

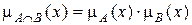где «×» – логическое умножение;

– объединение АÈВ или, если определить эту операцию через функ­цию принадлежности:

(1.28)

 

,

 

где «+» – логическое сложение.

Пример 1.2. Рассмотрим вышеприведенные операции на примере. Пусть имеются множество Е (1.22) и два его подмножества: А (которое уже было рассмотрено в предыдущем примере) и В:

А = {(х ₁,0), (х ₂,1), (х ₃,1), (х ₄,0), (х ₅,1)}, (1.29)

 

B = {(х ₁,1), (х ₂,0), (х ₃,1), (х ₄,0), (х ₅,1)}. (1.30)

 

Тогда операция пересечения будет выглядеть следующим образом:

 

А Ç В = {(х ₁,0 × 1), (х ₂,1× 0), (х ₃,1 × 1), (х ₄,0 × 0), (х ₅,1 × 1)}. (1.31)

 

Операция объединения соответственно будет записана так:

 

А È В = {(х ₁,0 +1), (х ₂,1+ 0), (х ₃,1+1), (х ₄,0 + 0), (х ₅,1+1)}. (1.32)

 

Знаки умножения и сложения соответствуют логическому И и логиче­скому ИЛИ.