Использовать надежностные характеристики объекта, заданные в виде таблицы, весьма неудобно. Поэтому по результатам эксперимента подбирают аналитическую формулу, которая наиболее удачно подходит в данном случае, и определяют коэффициенты этой формулы. Наиболее типичные формулы называются законами распределения случайных величин. Рассмотрим наиболее распространенные законы.
Показательное (экспоненциальное) распределение
Показательное распределение характерно тем, что интенсивность постоянна (l = const). Отсюда
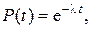
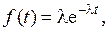
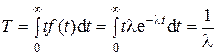. (2.16)
Примерный вид соответствующих кривых показан на рис. 2.2.
Рис. 2.2. Примерный вид основных показателей
надежности при экспоненциальном распределении
Показательное распределение применяется на практике очень широко. При этом отказы элементов рассматриваются как пуассоновский поток отказов, обладающий следующими свойствами: простейший (время между отказами распределено по экспоненциальному закону), ординарный (два события не могу произойти в один и тот же момент времени), стационарный без последействий.
Некоторые данные об интенсивности отказов компонентов вычислительных систем приведены в приложении.
Пример 2.2. Пусть в результате испытаний получены следующие значения:
| ti | |||||||||||
| N (ti) |
Проведя расчеты l i, видим, что l i» 0,05 и не зависит от ti. Следовательно, можно сделать вывод, что закон распределения надежности данного объекта является экспоненциальным, при этом l = 0,05. Тогда Т = = 1/l = 20 ч. Найдем Р (t) и Q (t) за 30 ч согласно (2.16):
Р (30) = е–0,05×30 = 0,223,
Q (30) = 1 – P (30) = 0,777
и за 100 ч:
Р (100) = е–5 = 0,067,
Q (100) = 1 – P (100) = 0,9933.
В теории надежности существует правило: считается, что распределение экспоненциальное, если результаты эксперимента явно этому не противоречат.
