Для расчета пластин можно использовать уравнения и формулы в размерном виде [1+4]. При этом рассчитывается конкретная пластина с заданными размерами a, b, h,(м), коэффициентом Пуассона μ, модулем упругости Е (Па) – (1 Па = 1 Н/м2), поперечной нагрузкой q (Па).
Однако возможно рассчитать пластину в безразмерном виде, при этом результаты одного конкретного расчета соответствуют многим реальным пластинам.
Для приведения к безразмерному виду уравнений и формул [1+4], описывающих поведение пластины под поперечной нагрузкой, необходимо на основе теории подобия ввести безразмерные переменные и функции по формулам
; 
; 
; 
; 
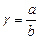(1)
,
где 
- характер изменения нагрузки вдоль оси 
,
- характер изменения нагрузки вдоль оси 
,
- цилиндрическая жесткость пластины.
При этом внешняя нагрузка представляется в виде
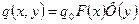, (2)
поэтому в (1) имеем 
.
Теперь пластина отнесена к безразмерным координатам , , 
, 
- рис.2.
Отношение 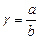характеризует отношение сторон пластины в плане, 
являются безразмерной поперечной активной нагрузкой, W(x,y) - безразмерный прогиб.
Также необходимо записать в безразмерном виде уравнение равновесия пластины и напряжения [1+4] для изгибающих Мx(x,y) и My(x,y) и крутящего Н(х,у) моментов и поперечных сил Qx(x,y) и Qy(x,y).
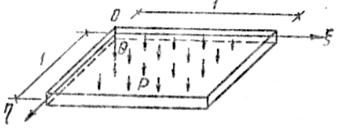
Рис.2
Необходимо помнить, что поперечные силы Qx, Qy и моменты Mx, My, H в пластинке являются погонными, т.е. приходящимися на единицу длины сечения пластинки и имеющего соответственно размерности Н/м, Нм/м.
Необходимо также обратить внимание на следующее: на контуре пластины поперечную силу Qx(x,y) (или Qy(x,y)) и крутящий момент Н(х,у) можно заменить статически им эквивалентной приведенной поперечной силой Q*x(x,y) (или Q*у(x,y)).
Подставляя формулы (1) в уравнение Софи Жермен и в выражения Мх, Му, Н, Q*x, Q*y [1+4], получим следующие выражения для уравнения равновесия в безразмерном виде и для безразмерных функций:
(3)
.
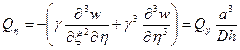
Предположим, что необходимо рассчитать пластину, определенным образом закрепленную по контуру (например, защемленную), с определенным видом распределения нагрузки (например, равномерным), причем параметры 
, 
. Если проводит расчеты в безразмерном виде, приняв 
, 
, то получим решение для пластины с произвольными величинами цилиндрической жесткости D, толщины h, размера в плане а, уровня нагрузки q. То есть результаты одного расчета в безразмерном виде соответствуют множеству реальных пластин, поэтому все дальнейшие расчеты проводим в безразмерном виде на основе формул (1) и (3).
