Вычисление момента в

При расчете тонкостенного стержня заменяем внешнею нагрузку P_i, q_i, линия действия которой не проходит через центр изгиба, такой же нагрузкой, проходящей через центр изгиба. При этом необходимо дополнить точенную нагрузку сосредото­ченными М_i или распределенными по длине m_i крутящими момен­тами, которые вычисляются то следующим формулам:

, ,

где е - расстояние от центра изгиба до центра тяжести. Знак крутящего момента М_i или m_i берется положительным, если при взгляде, со стороны положительного направления оси Z вращение происходят по часовой стрелке.

Под действием нагрузки, линия действия которой проходит через центр изгиба, стержень будет испытывать только попереч­ный изгиб. Для этого вида деформации определяются изгибающие моменты М_Х, и поперечные силы Q. Под действием крутящей нагрузки стержень будет испытывать изгибное кручение. Для этого вида деформации необходимо определить величины М₀=GJ_dθ’, B=-Eθ”J_ω и изгибно-крутящий момент M_ω=-Eθ’”J_ω.

Входящие в эти величины угол поворота поперечного сеченияего производные находятся из решения дифференциального уравнения равновесия тонкостенного стержня при кручении, которое имеет следующий вид:

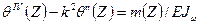. (4)

Здесь характеристика жесткости k(М^-1) вычисляется по формуле , где Е - модуль Юнга (Па), G - модуль сдвига (Па), J_d- момент инерции поперечного сечения при кручении (М²), m(Z)- интенсивное распределенного внешнего крутящего момента.