Для определения в пластине деформации и напряжений необходимо построить эпюры прогиба w, изгибающих Мξ, Мh и крутящего 
моментов, поперечных сил 
- рис.8. Для построения данных эпюр необходимо подставить выражение для 
(5) в формулы (3), в результате чего получим формулы для приведенных безразмерных моментов и поперечных сил:
Рис.8
(38)
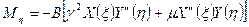
В расчетно-проектировочной работе необходимо построить эпюры, используя сетку координат ξ= 0, 0.25, 0.5, 0.75, 1.0: h= 0, 0.25, 0.5, 0.75, 1.0. Таким образом, необходимо найти значения каждой из функций (38) в 25 точках.
Рассмотрим пример построения эпюр для пластины (μ=0.3, γ=1), изображенной на рис.9.
Рис.9
Построенные для нее статическим методом В.З. Власова аппроксимирующие функции имеют вид:
, 
.
Производные от функци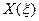и 
и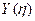 
имеют вид:
; 
; 
;
; 
; 
; 
;
.
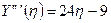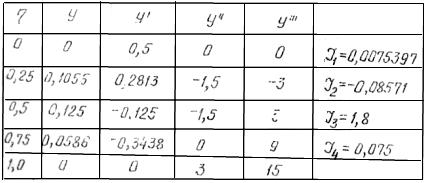
Значения функции 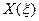и ее производных для пяти значений 
, а также величины I1, I2, I3, I4, указаны в таблице 1.
Таблица 1
Значения функции 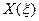и ее производных для пяти значений 
, а также значений 
указаны в табл.2.
Таблица 2
В процессе решения задачи методом Бубнова – Галеркина находим по формуле (37) амплитуду прогиба 
:
.
Для дальнейшего решения задачи принимаем Р0=10 и имеем поэтому В=0.237.
Далее по формуле (38) вычисляем значения функции w, , Мξ, Мh, для нашей сетки координат и по полученным значениям строим эпюры этих функций. На рис.10 приведены данные эпюры для В=1, т.е. эпюры w/B, 
, Мξ/В, Мh/В, 
.
Следует помнить, что на эпюрах положительные значения принято откладывать вверх, а положительные значения , Мξ, Мh - вниз.
Также следует помнить, что при выполнении расчетно-проектировочной работы требуется построить каждую из эпюр по 25 вычисленным значениям. Эпюры необходимо строить в большом масштабе.
Все значения, необходимые для построении эпюр, вычисляются с помощь. ЭВМ “Электроника” Д3-28 по прилагаемой ниже программе.
На основе полученных эпюр возможно определить значения нормальных 
, 
и касательного 
напряжений в конкретных точках любого слоя пластины. Наибольшие значения нормальных напряжений будут из нижней (знак «+» в формуле (39)) и на верхней (знак «-» в формуле (39)) поверхностях пластины
, 
, 
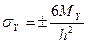(39)
Отметим, что переход от безразмерных к размерным функциям осуществляется на основе формул (3), например, для моментов имеет 
, 
.
При использовании энергетической теории прочности условие прочности рассматриваемых упругих пластин запишем в виде:
. (40)
где [σ] - нормативное напряжение для материала пластины.
Исследование влияния степени вытянутости плана
