θ0, θ’0, В0, Н0
Для нахождения уравнения (4) будем использовать метод начальных параметров [1]. В этом случае в системе координат OXYZ, связанной с центром тяжести крайнего левого сечения стержня, выражения для угла закручивания θ(Z), депланации θ’(Z), момента В(Z) и изгибно-крутящего момента Мω(Z) будут иметь следующий вид:
 (5)
(5)



Здесь  - начальные параметры, то есть значения искомых функций
- начальные параметры, то есть значения искомых функций  в сечении Z=0. Выражения для данных функций можно представить в виде матрицы начальных параметров, имеющей следующий вид:
в сечении Z=0. Выражения для данных функций можно представить в виде матрицы начальных параметров, имеющей следующий вид:

В выражениях (5)  зависят от величины действующих на стержень распределенных по длине mi(Z) и сосредоточенных Mi крутящих моментов и в обозначениях рис.6 имеют следующий вид:
зависят от величины действующих на стержень распределенных по длине mi(Z) и сосредоточенных Mi крутящих моментов и в обозначениях рис.6 имеют следующий вид:

Рис.6
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ;
;

Напомним, что соответствующие грузовые слагаемые  из выражений (5) учитываются лишь для сечений, расположенных правее приложения сосредоточенного момента Mi или начала участка действия распределенного по длине крутящего момента mi. Если распределенная по длине нагрузка заканчивается в некотором сечении ci, то ее условно продлевают до правого конца балки и одновременно с этим прикладывают, начиная с сечения, с координатой ci и до правого конца балки, нагрузку той же величины, но с обратным знаком. В том случае грузовые слагаемые, соответствующие распределенной крутящей нагрузке, действующей на участке от bi до ci, будут иметь вид:
из выражений (5) учитываются лишь для сечений, расположенных правее приложения сосредоточенного момента Mi или начала участка действия распределенного по длине крутящего момента mi. Если распределенная по длине нагрузка заканчивается в некотором сечении ci, то ее условно продлевают до правого конца балки и одновременно с этим прикладывают, начиная с сечения, с координатой ci и до правого конца балки, нагрузку той же величины, но с обратным знаком. В том случае грузовые слагаемые, соответствующие распределенной крутящей нагрузке, действующей на участке от bi до ci, будут иметь вид:
 (6)
(6)



Напомним, что знак для крутящих моментов Мi или mi берется положительным, если при взгляде со стороны положительного направления оси OZ вращение происходит по часовой стрелке. Сосредоточенный Мi и распределенные по длине mi крутящие моменты вычисляются по формуле:
 ,
,  , (7)
, (7)
где е - расстояние от центра тяжести до центра изгиба сечения.
Для нахождения значений начальных параметров  , входящих в выражения (5), используют условия закрепления стержня на его концах при Z=0 и Z=l.
, входящих в выражения (5), используют условия закрепления стержня на его концах при Z=0 и Z=l.
Если концевое сечение стержня защемлено, то для него имеем  ,
,  , если шарнирно закреплено, то получаем
, если шарнирно закреплено, то получаем  ,
,  . На свободном конце стержня должны выполняться условия
. На свободном конце стержня должны выполняться условия  ,
,  . Напомним, что через
. Напомним, что через  обозначается полный крутящий момент.
обозначается полный крутящий момент.
Для нагрузок рассматриваемых типов, приведенных и в задании на расчет стержня, выражение для Н можно представить следующим образом:
 .
.
Из условия  следует, что:
следует, что:
 (8)
(8)
Приведенные равенства позволяют найти значения двух начальных параметров непосредственно из условий при  , а для нахождения величин оставшихся двух начальных параметров необходимо составить и решить систему двух алгебраических уравнений. Например, для защемленного сечения
, а для нахождения величин оставшихся двух начальных параметров необходимо составить и решить систему двух алгебраических уравнений. Например, для защемленного сечения  граничные условия дают систему уравнений
граничные условия дают систему уравнений  ,
, 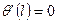 .
.
В качестве примера рассмотрим определение начальных параметров в стержне, изображенном на рис.4. На стержень действуют сосредоточенный М и распределенный по длине m крутящие моменты:







 .
.
В данном случае величина эксцентриситета равняется
 - см. [5], с. 20.
- см. [5], с. 20.
Тогда при значении характерного размера поперечного сечения
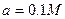 получим:
получим:


 .
. 

 .
.
На рис.7 изображен рассматриваемый стержень с действующими на него крутящими моментами

Рис.7
Граничные условия для этого стержня имеют вид:
 ,
,  ,
,  (9)
(9)
 ,
,  ,
,  (10)
(10)
Из условий (9) следует, что  ,
,  .
.
Соотношения (10)  и
и 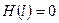 запишутся в виде:
запишутся в виде:


 (2м)=0.
(2м)=0.
Из второго соотношения (11) получаем значение начального параметра:
 МН М.
МН М.
Для вычисления входящей в выражение (11) изгибно-крутильной характеристики стержня  необходимо вычислить значение
необходимо вычислить значение  .
.
Величина  для поперечных сечений, состоящих из отдельных прямоугольных или криволинейных полос со сторонами
для поперечных сечений, состоящих из отдельных прямоугольных или криволинейных полос со сторонами  и соответствующими толщинами
и соответствующими толщинами  , определяется по формуле [1]:
, определяется по формуле [1]:
 (12)
(12)
Суммирование здесь распространяется на все прямоугольники и полосы, из которых состоит поперечное сечение.
Поправочный коэффициент  зависит от вида профиля поперечного сечения стержня и определяется экспериментальным путем. Ниже приведены значения
зависит от вида профиля поперечного сечения стержня и определяется экспериментальным путем. Ниже приведены значения  дня некоторых типов поперечных сечений:
дня некоторых типов поперечных сечений:
 для двутавров, причем среднее значение равняется
для двутавров, причем среднее значение равняется  ,
,
 для швеллеров, причем
для швеллеров, причем 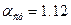 ,
,
 для уголков, причем
для уголков, причем 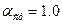 ,
,
 для
для  - образных сечений, причем
- образных сечений, причем  ,
,
 для тавровых сечений,
для тавровых сечений, 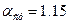 .
.
Отметим, что для поперечных сечений, приведенных в задании на работу, принимаем величину  , равной
, равной  .
.
Определим начальные параметры, используя соотношения [11], для стержня, изображенного на рис.3 методических указаний [5].
Примем для поперечного сечения  ,
,  , а также
, а также  . На основании выражения (12) получаем:
. На основании выражения (12) получаем:
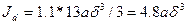 .
.
На основании использования выражения для 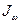 , приведенного на с. 22 методических указаний [5], имеем
, приведенного на с. 22 методических указаний [5], имеем  . Отсюда получаем величину:
. Отсюда получаем величину:
 .
.
Для величины  с учетом полученного значения
с учетом полученного значения  уравнения записываются следующим образом:
уравнения записываются следующим образом:
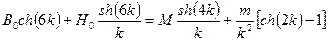 (13)
(13)
 МН М
МН М
Отсюда получаем значения начальных параметров:
 МН М2,
МН М2,  МН М.
МН М.
В качестве другого примера рассмотрим определение начальных параметров для стержня, изображенного на рис.5, поперечное сечение которого приведено на рис.13 методических указаний [5]. Для данного стержня на основании результатов расчета, приведенных на с. 23 [5], расстояние от центра тяжести изгиба равное  . Принимая
. Принимая  М, получим
М, получим  М. Тогда интенсивность распределенного крутящего момента составит:
М. Тогда интенсивность распределенного крутящего момента составит:
 МН М/ М.
МН М/ М.
На рис.8 показан рассматриваемый тонкостенный стержень с приложенной к нему крутящей нагрузкой.

Рис.8
Граничные условия для заданных закреплений концов стержня имеют вид:
при  :
:  .
.
 .
.
 :
:  .
.
Для определения начальных параметров 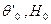 используются граничные условия (16) при
используются граничные условия (16) при  :
:
 (17)
(17)
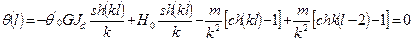
Отсюда система уравнений для определения 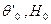 будет иметь следующий вид:
будет иметь следующий вид:

 .
.
Решая эту систему, находим  и
и  .
.
Отметим, что при определении начальных параметров следует проводить вычисления с особой тщательностью, удерживая 5-6 знаков после запятой, то есть использовать микрокалькулятор, считывая все цифры.
ПОСТРОЕНИЕ ЭРЮР УГЛА ЗАКРУЧИВАНИЯ  , ДЕПЛАНАЦИИ
, ДЕПЛАНАЦИИ  , БИМОМЕНТА
, БИМОМЕНТА  И ИЗГИБАЮЩЕГО-КРУТЯШЕГО МОМЕНТА
И ИЗГИБАЮЩЕГО-КРУТЯШЕГО МОМЕНТА 
После нахождения величин всех начальных параметров с использованием выражений (5) можно построить эпюры функций  ,
,  ,
,  ,
,  по длине балки. В качестве примера рассмотрим балку, изображенную на рис. 4, 7. Вид эпюр приведен на рис. 9. Вместо эпюр
по длине балки. В качестве примера рассмотрим балку, изображенную на рис. 4, 7. Вид эпюр приведен на рис. 9. Вместо эпюр  и
и  приведены эпюры
приведены эпюры  и
и  , ординаты которых используются при построении эпюр
, ординаты которых используются при построении эпюр 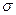 и
и  . Контролем правильности построения эпюр служит выполнение граничных условий при
. Контролем правильности построения эпюр служит выполнение граничных условий при  ,
,  . В данном случае при
. В данном случае при  должно получиться
должно получиться  ,
,  , а при
, а при  -
-  ,
,  .Контролем также может служить и вид эпюры
.Контролем также может служить и вид эпюры  , которая должна иметь постоянные ординаты на участках, где
, которая должна иметь постоянные ординаты на участках, где 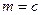 . Полезно также учитывать, что
. Полезно также учитывать, что  пропорционален
пропорционален  , а
, а  .
.
В конце методических указаний производится программа расчета, составленная на алгоритмическом языке “Бейсик” УКМЦ Электроника МС-0511. Приводится схема алгоритма и инструкция к программе, позволяющая вычислять ординаты эпюр  ,
,  ,
, 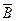 ,
,  .
.

Рис.9
ПОСТРОЕНИЕ ЭПЮР НОРМАЛЬНЫХ  ,
, 






