Пример 1. В электроцехе энергетического предприятия имеется 5 ремонтных бригад (n = 5 каналов). В электроцех поступает простейший поток заявок на ремонт с плотностью λ = 4 заявки в месяц. Средняя продолжительность ремонта T0 = 1месяц. Определить вероятность образования очереди на ремонт.
Решение
Найдем приведенную плотность потока заявок α= λ/μ=λТ0=4∙1=4.
По формуле Ротк = 
Р0ТК. = 45/[5! (1+ 4/1+ 42/2! + 43/3! + 44/4! + 45/5!)] = 0,16.
Отметим, что при заданной вероятности отсутствия очереди на ремонт,известных интенсивности отказов электрооборудования и средней продолжительности ремонта единицы электрооборудования можно определить оптимальное количество ремонтных бригад.
Рассмотрим расчет показателей надежности восстанавливаемых СМО.
Количественные характеристики показателей надежности зависят от состояния системы в каждый момент времени. Процессы изменения состояний системы, на которые в основном влияют случайные отказы отдельных элементов, описываются с использованием пуассоновских случайных процессов (редкие случайные явления). При экспоненциальном распределении времен между отказами и ремонтами используются марковские случайные процессы
Математический аппарат для анализа надежности восстанавливаемых СМО разработан на основе марковской модели с дискретным множеством состояний и непрерывным временем [4,5,7]. Для этого необходимо, чтобы потоки, переводящие систему из состояния в состояние, были пуассоновскими, а законы распределения наработки до отказа и времени восстановления были бы экспоненциальными. Структуры системы изображается в виде графов состояний с прямыми (отказ) и обратными (ремонт) переходами.
Обычно рассматриваются марковские процессы у которых для любого момента времени вероятность каждого состояния элемента (системы) в будущем зависит только от состояния в настоящий момент, и не зависит от того, каким образом элемент (система) пришел в это состояние.
Использования марковских случайных процессов в системах электроснабжения подтверждается практикой их эксплуатации.[6].
Действительно, в большинстве случаев, каждый элемент системы является достаточно надежным и отказывает сравнительно редко. Поток отказов каждого элемента образуется из суммы потоков его конструктивых частей. Эти потоки независимы. Аналогичный вывод можно сделать о системе электроснабжения в целом. Если не рассматривать каскадное развитие аварии, то появление отказа элемента на одном интервале времени почти не влияет на появление отказов в другое время. Поэтому поток отказов таких элементов системы в целом можно рассматривать как пуассоновский.
В периоды приработки, интенсивного износа и старения потоки отказов элементов не обладают марковским свойством. Но на практике продолжительность этих периодов сокращается за счет проведения испытаний ответственных элементов системы до начала эксплуатации и плановой замены морально устаревшего и изношенного оборудования.
Исходя из вышеизложенного, рассмотрим математические модели, отвечающие нормальному периоду эксплуатации элементов (подсистем), что представляет наибольший практический интерес.
Порядок исследования системы с использованием марковских случайных процессов:
1. Вводится понятие состояния системы. В данном случае это будет чередующийся процесс отказов и восстановлений системы.
2. Описываются все состояния системы, в которых она может находиться. Множество состояний системы представляется в виде вектора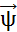 
= < 0, 1,..., b >.. При этом N = b + 1 - общее число состояний системы.
3. Составляется граф состояний системы в следующем виде (рис.4.1).
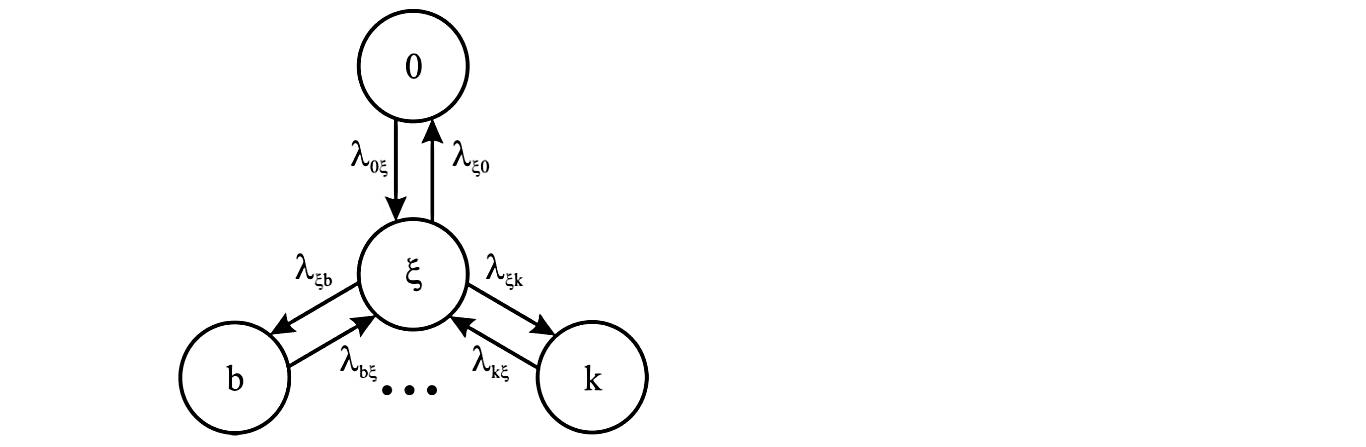
Рисунок 4.1. Граф состояний системы
4. Определяется вектор начальных условий
(0) = P0= < P0(0),Р1(0),..., Рb(0) >.
5.Для каждого возможного перехода указывается интенсивность λξk.. Составляется матрица переходов Λ = || λξk.||NN.
6.Вводится вектор вероятности состояния: (t) = < Р0 (t), Р1, (t),..., Pb(t)>, где Ρζ - вероятность пребывания системы в ξ- м состоянии в момент времени t. Поскольку события, отображающие вероятности Ρζ (t), образуют полную группу, то 
= 1 рассматривается как нормировочное уравнение. Задача сводится к определению вектора переходных вероятностей, который позволяет рассчитать необходимые показатели надежности.
7.Составляется система дифференциальных уравнений Колмогорова
dPξ(t) / dt = ‑Pξ(t) 
ξk + ξkPk(t), (4.9)
k= 1, 2,…,b; Pξ(0) = Pξ0.
Уравнение Колмогорова в матричной форме имеет вид
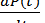=αP(t),P(0)=P0, (4.10)
где α = || 
.||NN, αξk = 
или используя условие нормировки, после преобразования, получим
= βp(t) = C, (4.11)
где β = || 
.||bb, = 
C = 
λ01, λ02,…,λob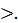 
8. Решается система дифференциальных или алгебраических уравнений (в случае установившегося процесса, dP/dt=0).Уравнение Колмогорова представляет собой систему обыкновенных линейных дифференциальных уравнений. Решение такой системы уравнений может быть выполнено на ЭВМ.
Для практических целей удобно решать систему дифференциальных уравнений на основе преобразования Лапласа. После операторного преобразования Лапласа уравнение Колмогорова примет вид
sР(s) = βР(s) ‑ Р (0), (4.12)
где Р (s) - матрица-столбец искомых вероятностей;
β - матрица коэффициентов переходов; Р (0) - матрица-столбец начальных значений вероятностей.
Решение уравнения (4.12)
Р (s) = [sI – β]-1 Р (0), (4.13)
где I - единичная матрица.
9.На практике процесс функционирования систем электроснабжения длится в течении нескольких лет. Таким образом можно перейти к предельным вероятностям. При существовании предельного стационарного режима система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени, то есть каждое из состояний осуществляется с некоторой постоянной вероятностью, представляющей не что иное, как среднее относительное время пребывания системы в данном состоянии. Вектор финальных вероятностей, характеризующих стационарный режим
=<Р1∞,Р2∞,…,Рb∞>, (4.14)
Где Pξ∞ = lim Pξ(t), ζ= 1,2,…,b определяется укороченным уравнением Колмогорова.
βР∞ = ‑С. (4.15)
Это уравнение с учетом того, что 
позволяет найти вероятности всех состояний.
10.Рассчитав вероятности состояний находим показатели надежности.
Рассмотрим вопросы оценки надежности восстанавливаемых систем электроснабжения с учетом специфики их эксплуатации.
