Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона

Ранее предполагалось, что закон генеральной совокупности известен. Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т. е. при помощи специально подобранной случайной величины — критерия согласия.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия: («хи квадрат») К. Пирсона, Колмогорова, Смирнова и др.

Рассмотрим применение критерия Пирсона [3] к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется и для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Обычно эмпирические и теоретические частоты различаются, например

эмп. частоты 6 13 38 74 106 85 30 10 4

теорет. частоты 3 14 42 82 99 76 37 11 2

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что тео­ретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Итак, пусть по выборке объема n получено эмпирическое распределение:

варианты x_i x₁ x₂... x_s

эмп. частоты n_i n₁ n₂ n_s

Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты (например, так, как в 3.4.4.). При уровне значимости α требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величин

= , ∗

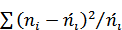– эмпирические частоты; 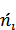‑ теоретические частоты.

Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (∗), и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. Делением на 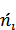достигают уменьшения каждого из слагаемых; в противном случае сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. Разумеется, приведенные соображения не являются обоснованием выбранного критерия, а лишь пояснением.

Доказано, что. при n→∞ закон распределения случайной величины (∗) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ² c k степенями свободы. Поэтому случайная величина (∗) обозначена через χ² а сам критерий называют критерием согласия «хи квадрат».

Число степеней свободы находят по равенству k = s – 1 – r, где s - число групп (частичных интервалов) выборки; r -число параметров предполагаемого распределения, которые оценены по данным выборки.

В частности, если предполагаемое распределение нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому r = 2 и число степеней свободы k = s – 1 – r = =s – 1‑2=s‑3.

Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр λ, поэтому r = =1 и k = s ‑ 2.

Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α

P[χ² > χ²_кр (α; k)] = α.

 

Таким образом, правосторонняя критическая область определяется неравенством χ² > χ²_кр (α; k), а область принятия нулевой гипотезы ‑ неравенством χ² < χ²_кр (α; k).

Обозначим значение критерия, вычисленное по данным наблюдений, через χ²_набл. и приведем правило проверки нулевой гипотезы.

Правило. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H₀: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия

= (**)

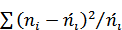и по таблице критических точек распределения χ² (см. таблицу приложения 2), по заданному уровню значимости α и числу степеней свободы k = s - 3 найти критическую точку χ²_кр (α; k).

Если χ²_набл < χ²_{кр -} нет оснований отвергнуть нулевую гипотезу.

Если χ²_набл > χ²_{кр -} нулевую гипотезу отвергают.

Замечание 1. Объем выборки должен быть достаточно велик, во всяком случае не менее 50. Каждая группа должна содержать не менее 5—8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.

Замечание 2. Поскольку возможны ошибки первого и второго рода, в особенности если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс.

Замечание 3. Для контроля вычислений формулу (**) преобразуют к виду

χ²_набл = [Σ(n²_i/ n_i')] ^_ n.

Рекомендуем выполнить это преобразование самостоятельно, для чего надо в (**) возвести в квадрат разность частот, сократить

результат на n_i' и учесть, что Σn_i = n, Σn_i' = n.

Пример решения задачи к разделу 3.4.3. [3 ]

 

Пример 4. При уровне значимости α =0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

эмп. частоты 6 13 38 74 106 85 30 14

теорет. частоты 3 14 42 82 99 76 37 13

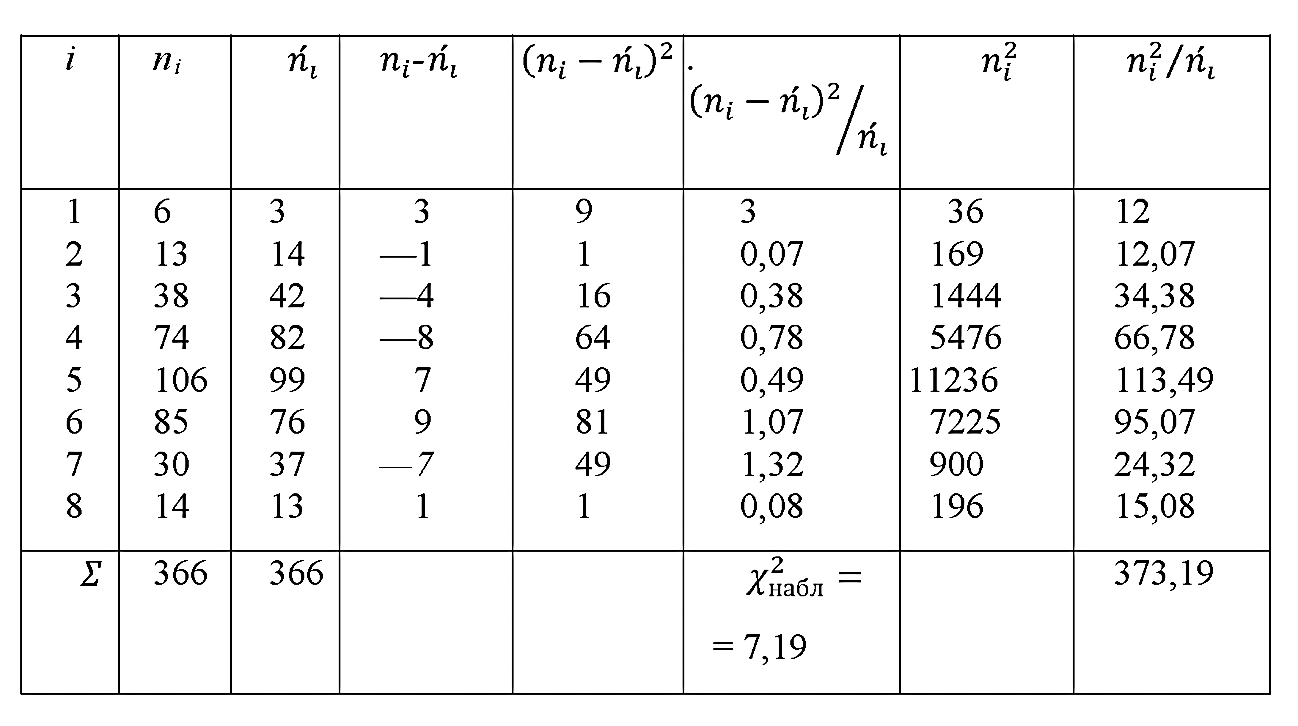
Решение. Вычислим χ²_набл, для чего составим расчетную табл. 3.2.

Контроль: χ²_набл = 7,19: [Σ(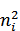 _/n_i')]-n = 373,19 — 366 = 7,19. Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число различных вариант s = 8; k = 8 ‑ 3 = 5.

По таблице критических точек распределения χ² (см. табл. приложения 2, по уровню значимости α = 0,05 и числу степеней свободы к = 5 находим χ²_кр (0,05; 5)= 11,1.

Так как χ²_набл < χ²_кр — нет оснований отвергнуть нулевую гипо­тезу. Другими словами, расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

 

Таблица 3.2.