Порядок исследования остается тем же. При этом, кроме коэффициента готовности и коэффициента простоя, рассматриваемых в качестве основных показателей для таких объектов, используется функция надежности, (вероятность того, что в интервале времени 0, t не произойдет отказа), а также наработка до отказа (в этом случае имеется «поглощающее» состояние и необходимо решить полную систему дифференциальных уравнений при соответствующих начальных условиях). В отдельных задачах определяется также средний период ремонтов.
В электроснабжении наиболее часто применяется однократное резервирование, поэтому вначале рассмотрим дублирование многократно используемого электротехнического агрегата с одной ремонтной бригадой при ненагруженном и нагруженном резервировании.
В этом случае будет три состояния системы:
0- оба агрегата работоспособны;
1- один агрегат восстанавливается, а другой работает;
2- оба агрегата восстанавливаются
Структурная схема состояний системы для рассматриваемого случая приведена на рисунке 4.5.
Рисунок 4.5. Граф переходов дублированной системы
Решение уравнения Колмогорова в случае стационарного режима (при t→ ∞) определяет формулы для вероятностей состояния
P0 = 1 - 
, (4.28)
P1 = 1 - 
, (4.29)
P2 = 1 - 
, (4.30)
где ν=1 ‑ соответствует нагруженному резерву;
ν=0 ‑ ненагруженному резерву.
Коэффициент готовности определяется по формуле
KГ=1 – P2 =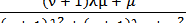 
. (4.31)
Сравнивая коэффициенты готовности дублированной системы при нагруженном и ненагруженном резерве можно показать, что выигрыша в надежности почти не происходит.
Примеры решения задач к разделу 4.3 [21]
Пример 3. В трансформаторной подстанции установлены рабочий и резервный трансформаторы, находящиеся в нагруженном резерве. Интенсивность отказов каждого трансформатора λ = 0,4 • 10-5 ч-1, а интенсивность восстановления μ = 0,5 ч-1. Определить коэффициент простоя.
Решение.
Трансформаторная подстанция в любой момент времени может находиться в одном из следующих состояний:
0- оба трансформатора работоспособны, 1- отказал один трансформатор, 2- отказали оба трансформатора.
Граф состояний трансформаторов ТП представлен на рис.5.6.
Рисунок 4.6. Граф состояний трансформаторов ТП.
Рисунок 5.12- Граф состояний трансформаторов ТП
|
При нахождении в состояниях 0 и 1 электроустановка работоспособна, в состоянии 2 - неработоспособна. Ниже приводится система дифференциальных уравнений.
Решим полученную систему при начальных условиях Р0 (0) = 1, P1(0) = Р2 (0) = 0. Переходя к изображениям, получим следующую систему алгебраических уравнений
Для получения величины Рi(ε) используем правило Крамера. При этом, Рi(ε)= Di/D, где D - определитель, элементами которого являются коэффициенты при Р0(ε), Р1(ε), Р2(ε); Di - определитель, который образуется путем замены i-гo столбца коэффициентами правой части уравнения.
В рассматриваемом случае необходимо определить функцию простоя, равную Р2 (t). Для этого запишем определители D и D2.
D =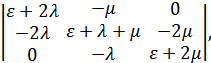 
D2 =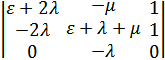 
.
В результате получим:
Р2 ( 
) =2λ2/ [ε2 + 3(λ + μ)ε + 2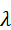 
2 + 4λμ + 2 
2].
Переходя от изображения к оригиналу, получим
KП (t) = Р2 (t) = λ2/(λ+μ)2{ 1‑2 ехр [- ( 
+ μ)t] + ехр [‑2( + (μ)t]}.
При t →∞ имеем:
KП = λ2/(λ+μ)2 = (4 • 10-3)2(4 • 10-3 + 0,5)2= 1,57 •10-2.
Пример 4. Написать выражение для определения коэффициента простоя системы электроснабжения объекта, имеющего ненагруженный резерв (дизельную электростанцию). Рассмотреть установившийся режим.
Решение.
Схема состояний для данной системы электрооборудования имеет вид (риc. 4.7.).
Рисунок 4.7. Граф состояний системы электроснабжения
Система алгебраических уравнений для установившегося режима с учетом нормировочного уравнения имеет вид
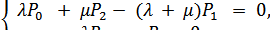
Решив уравнение методом подстановки, получим
KГ = Р0 + Р1 = (μ2 + λμ)/(μ2 +λμ + λ2).
При многократном резервировании получаемый набор агрегатов следует рассматривать как систему массового обслуживания, в которой поток заявок на обслуживание представляет собой поток отказов, а каналами являются ремонтные бригады [19]. Граф состояний такой системы показан на рисунке 4.8.
Рисунок 4.8. Граф состояний многократно резервируемого электротехнического агрегата
Значение коэффициента готовности определяется по следующим аналитическим зависимостям:
при ненагруженном резерве
KГ= 1 ‑ 
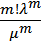. (4.32)
при нагруженном резерве
KГ = 1 ‑ 
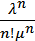. (4.33)
Для оценки надежности при скользящем резервировании рассмотрим систему из n независимых однотипных элементов и m незакрепленных резервных элементов. В этой ситуации может быть сформулировано несколько задач определения надежности, однако для нас наибольший интерес представляет определение коэффициента готовности системы многократного использования с нагруженным или ненагруженным резервом и одной ремонтной бригадой. Возможные состояния такой системы ψ = 0, 1,..., n + m. Решение системы уравнений Колмогорова для стационарного режима позволит определить аналитические зависимости для коэффициента готовности:
при нагруженном резерве
Кг = 
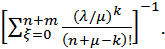(4.34)
при ненагруженном резерве
Кг = 
(4.35)
Помимо резервирования однотипными элементами с одинаковыми значениями λ и μ довольно часто применяется общее резервирование, а также параллельное включение агрегатов различной физической природы, например, госсеть резервируется дизельной электростанцией или аккумуляторной батареей, или тем и другим, что приводит к необходимости рассмотрения на основе марковского процесса различных ситуаций.
Рассмотрим типовые случаи резервирования.
1. Электроснабжение осуществляется от госсети с показателями надежности λ1 и μ1, в качестве резервного источника используется дизельная электростанция в ненагруженном резерве (имеющая в рабочем состоянии показатели надежности λ2 и μ2), при этом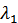 
> 
и 
< 
- Восстановление неограниченное Схема состояний представлена на рисунке 4.9.
Рис. 4.9. Схема состояний источников питания системы электроснабжения
Матрица вероятностей переходов из состояния 0 в 1 и из 1 в 2 имеет вид (при t: 
)
P∞ =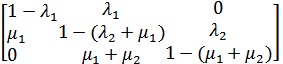 
• 
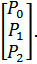
Для определения функции готовности системы электроснабжения решим следующую систему уравнений
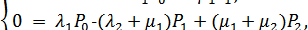(4.36)
При начальных условиях Р0(0) = 1, то есть оба источника исправны, с учетом нормировочного уравнения Р0 + Р1 + Р2= 1, решая систему уравнений (4.36), получим
КГ(∞) = 
. (4.37)
При использовании источников питания в нагруженном резерве матрица вероятностей переходов примет следующий вид (при t→∞)
P∞ =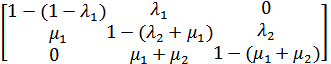 
• 
.
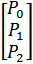Переходя к системе алгебраических уравнений, получим
(4.38)
Заменив одно из уравнений нормировочным Р0 + Р1 + Р2 = 1, в результате решения системы уравнений определяем коэффициент готовности
Кг∞ = 
, (4.39)
где 
.
Пример решения задачи с многократным резервированием без восстановления отказавших элементов [21]
Пример 5. Резервированная система состоит из основного элемента Э1 и двух резервных элементов Э2 и Э3. При отказе основного элемента в работу включается элемент Э2, при отказе Э2 — Э3. В выключенном состоянии резервный элемент отказать не может. Интенсивность потока отключений основного элемента λ1 резервных элементов в рабочем состоянии - λ2. Поток отказов простейший. Определить надежность системы в различных состояниях.
Решение.
Процесс, протекающий в системе, будем рассматривать марковским с непрерывным временем и дискретными состояниями. Система имеет 4 состояния:
0- работает основной элемент Э1
1- работает резервный элемент Э2,
2- работает резервный элемент Эз,
3- не работает ни один элемент.
Граф состояний системы показан на рисунке 4.10.
Рисунок 4.10. Граф состояний системы
|
Так как восстановление элементов не происходит, все стрелки на графе направлены в одну сторону.
Система уравнений Колмогорова для вероятностей состояний имеет вид
Нормировочное уравнение Р0 + Р1 + Р2 + Р3 = 1.
Из первого выражения определим Р0 (t) как функцию t Р0 (t) = 
. При этом начальное условие интегрирования Р0 (0) = 1. Подставляя полученное выражение во второе уравнение, получим
(t) = ‑ λ2Р1 +λ1 
Проинтегрируем это уравнение с начальным условием Р1(0) = 0. В результате получим
P1(t) = 
‑ 
Эту функцию подставим в третье уравнение, получим
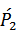(t) =‑ λ2Р2 (t) +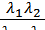 
‑
В результате интегрирования последнего выражения при начальном условии Р2 (0) = 0 имеем
P2(t) = 
+ 
‑ 
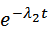Функцию Р3(t) найдем используя общее нормировочное уравнение
P0+ P1+ P2+ P3 = 1.
P3 = 1‑P0(t)–P1(t)–P2(t) = 1 –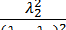 
– 
Для систем электроснабжения отдельных объектов характерно применение более сложных вариантов использования электроустановок (основной источник питания и дублированный резервный источник в ненагруженном резерве). При выходе из строя основного источника питания включается первый, а при выходе его из строя включается второй резервный источник питания. Такая схема с использованием внешней сети и дизельной электростанции с двумя агрегатами в режиме ненагруженного резерва широко применяется на узлах связи.
Рисунок 4.11. Схема состояний источников питания
(схема «гибели и размножения)
Схема состояний источников питания (рисунок 4.11.) представляет непрерывную марковскую цепь, именуемую схемой «гибели и размножения».
Матрица вероятностей переходов такой схемы может быть представлена в следующем виде:
P∞ = 
• 
.
Используя ее, можно составить систему уравнений
(4.40)
На основании известных зависимостей, описывающих решение задачи «гибели и размножения» в общем виде [21], найдем решение для частного случая, определив коэффициент готовности источника питания по формуле
Kг∞ = P0 + P1 + P2 =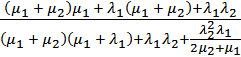 
. (4.41)
Для некоторых типов систем электроснабжения характерно другое сочетание элементов (дублированный основной источник питания и резервный источник в ненагруженном резерве).
Схема состояний для этого случая показана на рисунке 4.12.
Рис.4.12. Схема состояний системы, состоящей из дублированного основного и резервного источника питания
Возможными состояниями системы являются следующие:
0- все три источника исправны;
1- отказал один основной источник, включился равно надежный источник из ненагруженного резерва, первый источник восстанавливается;
2- отказал второй основной источник питания, работает резервный с характеристиками основного, два первых источника восстанавливаются;
3- все три источника восстанавливаются.
Матрица вероятности переходов для такой системы будет выглядеть следующим образом (при t →∞)
P∞ = 
• 
.
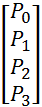Система уравнений (при t→∞)
Решение данной системы уравнений позволяет определить коэффициент готовности
КГ∞ = 
. (4.43)
Для электроснабжения ответственных потребителей в составе системы электроснабжения могут применяться установки гарантированного питания (УГП). В этом случае после включения система электроснабжения должна проработать безотказно заданное время, которое обычно определяется промежутком между профилактическими проверками. Для такой системы возникает задача определения вероятности того, что в пределах заданной наработки отказ не возникает, то есть определение вероятности безотказной работы (для рассматриваемых систем неработоспособное состояние является поглощающим).
Методический подход к решению задачи сохраняется В качестве примера рассмотрим расчет электроснабжения с гарантированным питанием потребителя с непрерывным производством.
Пример решения задачи расчета надежности электроснабжения с гарантированным питанием потребителя и непрерывным производством [21]
Пример 6. Система гарантированного питания потребителя с непрерывным процессом производства состоит из двух дизель - генераторов, находящихся в ненагруженном резерве. Интенсивность отказов и восстановления дизель - генератора в рабочем состоянии λ = 4 • 
ч‑1 и μ = 5 ч‑1. При одновременном отказе обоих источников система гарантированного питания неработоспособна. Необходимо определить наработку до отказа установки гарантированного питания.
Решение.
Возможные состояния установки гарантированного питания:
0 оба дизель - генератора работоспособны,
1 один из агрегатов неработоспособен,
2- оба агрегата вышли из строя.
Граф состояний системы показан на рисунке 4.13.
Рисунок 4.13. Граф состояний установки гарантированного питания
Система дифференциальных уравнений для данной схемы имеет вид
Начальные условия Р0 (0) = 1, P1 (0) = Р2 (0) = 0. Решив систему уравнений, получим выражения для вероятности попадания в поглощающее состояние Р2 (t) и для вероятности безотказной работы за это время 
(t)
P2(t) = 1 ‑ 
,
(t) = ,
Где 
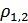= 0,5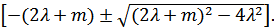 
Средняя наработка до отказа
T1 =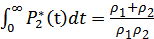 
= 
=3175 час.
В заключении необходимо отметить, что для точной оценки надежности сложной восстанавливаемой системы электроснабжения надо рассматривать 
состояний, что приводит к большому объему вычислений. Для уменьшения числа состояний используется несколько методов, основанных на исключении маловероятных состояний. Для этого вводят следующие допущения [6]: элементы электроснабжения имеют высокую надежность, их коэффициенты надежности близки к единице; наработка на отказ любого элемента многим больше времени их ремонта. При таких допущениях процесс эксплуатации системы электроснабжения представляется в виде узких импульсов (время ремонта), разделенных интервалами наработок на отказ. С учетом выше изложенного применяется приближенный метод оценки показателей надежности.
Суть метода заключается в условном объединении в эквивалентный элемент двух любых связанных между собой элементов электроснабжения. Полученный таким образом эквивалентный элемент характеризуется новым процессом функционирования с другими импульсами и интервалами,а следовательно со своими показателями надежности, которые рассчитываются по приведенным выше формулам. В результате такого объединения система, состоящая из n элементов приводится к системе из n‑1 элементов и т. д. до приведения к одному эквивалентному элементу.
Рассчитываются показатели надежности этого эквивалентного элемента, которые и будут приближенными оценками показателей надежности сложной системы электроснабжения.
