Безотказной работы

Наиболее распространенной характеристикой элемента электроснабжения является закон распределения среднего времени наработки на отказ T_ср:

Q(t) = Р (Т_ср < t).

Проверка выдвинутой гипотезы производится методами математической статистики с помощью так называемых критериев согласия. Гипотеза о виде закона распределения или гипотеза о постоянстве среднего значения какой-либо случайной величины выдвигаются на основании каких-либо теоретических предположений. Простейшим способом проверки является графический. Для графического сравнения опытных данных с теоретическими строят график теоретической функций и наносят ее значения, полученные из опыта. Пример такого построения для функции распределения Q (t) приведен на рис.3.10. [9].

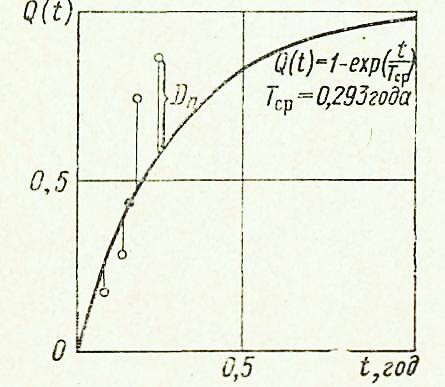
Рис.3.10. Проверка гипотезы о законе распределения

по критериюА.Н. Колмогорова

Здесь значения функции, полученные из опыта, отмечены кружками, а сплошной линией показана теоретическая кривая распределения. Графический метод весьма нагляден, но не позволяет измерить степень соответствия или согласия.

Количественная оценка согласия может быть сделана с помощью критерия А. Н. Колмогорова. Для применения этого критерия необходимо иметь значения теоретической и опытной функций для некоторого числа n значений аргумента. Из этих значений определяют максимальное значение расхождения между теоретическими и опытными данными

D_n= max| (t)– Q(t) |,

где (t) — значение интегральной функции распределения, полученное из опыта; Q(t) —теоретическое значение интегральной функции распределения. А.Н.Колмогоров доказал, что случайная величина D_n = Λ имеет функцию распределения

К (λ) = 1 ‑ р (λ) = ехр (‑2k²λ²).

Величины p(λ) для некоторых значений λ приведены ниже.

λ	p (λ)	λ	p (λ)	λ	p (λ)
0,0	1,0	0,7	0,711	1.4	0,040
0.1	1,0	0,8	0,544	1,65	0,022
0,2	1.0	0,9	0,398	1,6	0,012
0,3	1.0	1,0	0,270	1,7	0,006
0,4	0,997	1,1	0,178	1,8	0,003
0,5	0,964	1.2	0,112	1.9	0,002
0,6	0,864	1.3	0,068	2,0	0,001

Получив в результате сравнения функций , Q и вычислив D_n = λ можно по этой таблице оценить вероятность случайного получения подобного значения λ.

Если р (λ) >0,3—0,4, то считают, что опытная и теоретическая функции хорошо согласуются между собой, если р(λ)< 0,05—0,1, то это означает, что наблюдаемое отклонение не случайно, т. е. теоретическая функция плохо согласуется с опытными данными.

Необходимо отметить, что критерий согласия А. Н. Колмогорова предполагает теоретическое распределение известным из каких-либо предпосылок теоретического характера. Кроме того, в случае определения параметров теоретической функции из опыта он дает завышенную оценку согласия.

Пример решения задачи к разделу 3.4.2 [9 ]

Пример 3. Проверим соответствие гипотезы об экспоненциальном распределении данных о повреждениях на линии электропередачи 220 к В. Исходные данные и необходимые расчеты сведены в табл. 3.1.

Проверка гипотезы экспоненциального закона

Таблица 3.1

i	t,лет	m_i	=m_i_/n	= _i	t_i_/T_СР	Q=exp- (t_i_/T_СР)	D(t)
	0,091		0,143	0,143	0,310	0,265	0,122
	0,143		0,143	0,286	0,488	0,385	0,099
	0,167		0,143	0,429	0,570	0,435	0,006
	0,200		0,286	0,715	0,682	0,495	0,220
	0,250		0,143	0,858	0,853	0,575	0,283
	1,000		0,143	1,000	3,413	0,965	0,035

n = _i = 7; T_ср = _i m_i = 0,292,

где t_i - время безотказной работы, т_i — количество наблюдений.

Максимальному отклонению D_n = 0,283 при 7 наблюдениях соответствует λ_n=0,283 =0,75 и р (0,75) =0,63. Эта вероятность достаточно велика, что позволяет считать отклонение случайным, а гипотезу об экспоненциальном законе распределения не противоречащей полученным данным.