В математической статистике используется несколько критериев однородности [8]: критерий знаков, Вилкоксона, Пирсона, Ван-дер-Вардена, Смирнова. Первые четыре критерия менее трудоемки, но при этом имеют меньшую чувствительность (мощность). Ограничимся рассмотрением критерия Вилкоксона. [3]
Критерий Вилкоксона служит для проверки однородности двух независимых выборок: x1, х2 ,..., хп и у1, y2, …, yn. Достоинство этого критерия состоит в том, что он применим к случайным величинам, распределения которых неизвестны; требуется лишь, чтобы величины были непрерывными.
Если выборки однородны, то считают, что они извлечены из одной и той же генеральной совокупности и, следовательно, имеют одинаковые» причем неизвестные, непрерывные функции распределения F1(х) и F2(х).Таким образом, нулевая гипотеза состоит в том, что при всех значениях аргумента (обозначим его через х) функции распределения равны между собой:
F1(х)=F2(х).
. Конкурирующими являются следующие гипотезы:
F1(х)=F2(х),F1(х)>F2(х). и F1(х) <F2(х).
Заметим, что принятие конкурирующей гипотезы
Н1: F1(х) <F2(х)означает, что X > У.
Действительно, неравенство F1(х)<F2(х) равносильно неравенству Р (X < х) < Р (У < х). Отсюда легко получить, что Р (X > х) > Р (У > x). Другими словами, вероятность того, что случайная величина X превзойдет фиксированное действительное число х, больше, чем вероятность случайной величине У оказаться большей, чем х; в этом смысле X > У.
Аналогично, если справедлива конкурирующая гипотеза H1: F1(х)> F2(х), то X < У.
Далее предполагается, что объем первой выборки меньше (не больше) объема второй: n1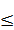 
n2 если это не так, то выборки можно перенумеровать (поменять местами).
А. Проверка нулевой гипотезы в случае, если объем обеих выборок не превосходит 25.
Правило 1. Для того чтобы при заданном уровне значимости α = 2Q проверить нулевую гипотезу Н0: F1(х)= F2(х) об однородности двух независимых выборок объемов n1 и n2 (n1 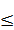n2) при конкурирующей гипотезе Н1: F1(х) 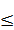F2(х), надо:
1)расположить варианты обеих выборок в возрастающем порядке, т. е. в виде одного вариационного ряда, и найти в этом ряду наблюдаемое значение критерия Wнабл. ‑ сумму порядковых номеров вариант первой выборки;
2)найти по таблице приложения 3 нижнюю критическую точку w нижн.кр (Q; n1, n2), где Q =α/2;
3)найти верхнюю критическую точку по формуле
W верхн.кр =(n1 + n2+ 1) n1 ‑ w нижн.кр.
Если W набл. < w нижн.кр или W набл. > w верхн.кр —нулевую гипотезу отвергают.
Если w нижн.к < W набл. < w верхн.кр - нет оснований отвергнуть нулевую гипотезу.
Пример решения задачи к разделу 3.4.1. [3 ]
(для случая, если объем обеих выборок не превосходит 25)
Пример 1. При уровне значимости 0,05 проверить нулевую гипотезу об однородности двух выборок объемов n1 =6 и n2 = 8:
xi 15 23 25 26 28 29
yi 12 14 18 20 22 24 27 30
при конкурирующей гипотезе Н1: F1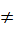(х) 
F2(х)
Решение. Расположим варианты обеих выборок в виде одного вариационного ряда и перенумеруем их:
порядковые номера 1 2 3 4 5 6 7 8 9 10 11 12 13 14
варианты… 12 14 15 18 20 22 23 24 25 26 27 28 29 30
Найдем наблюдаемое значение критерия Вилкоксона — сумму порядковых номеров первой вариант первой выборки:
Wнабл. = 3+7+9 +10+12 +13 = 54.
Найдем по таблице приложения 3 нижнюю критическую точку, учитывая, что Q= α/2 = 0,05/2 = 0,025, n1 =6, n2 =8
W нижн.кр (0,025; 6, 8) = 29.
Найдем верхнюю критическую точку:
W верхн.кр = (n1+ n2+1) n1 - w верхн.кр = (6 + 8+1)٠6 – 29 = 61.
Так как 29 < 54 < 61, т. е w нижн.кр < Wнабл. < w верхн.кр — нет оснований отвергнуть нулевую гипотезу об однородности выборок.
Правило 2. При конкурирующей гипотезе F1(х) > F2 (х) надо найти по таблице нижнюю критическую точку w нижн.кр (Q; n1, n2), где Q =α.
Если Wнабл. > w нижн.кр —нет оснований отвергнуть нулевую гипотезу.
Если Wнабл. < w нижн.кр —нулевую гипотезу отвергают.
Правило 3. При конкурирующей гипотезе Н1: F1(х)<F2(x) надо найти верхнюю критическую точку: w верхн..кр (Q; n1, n2)= (n1 + n2+ 1) n1 ‑ w нижн.кр (Q; n1, n2), где Q =α
Если Wнабл. < wверхн.кр ‑ нет оснований отвергнуть нулевую гипотезу.
Если Wнабл. > wнижн.кр ‑ нулевую гипотезу отвергают.
Замечание. Если несколько вариант только одной выборки одинаковы, то в общем вариационном ряду им приписывают обычные порядковые номера (совпавшие варианты нумеруют так, как если бы они были различными числами); если же совпадают варианты разных выборок, то всем им присваивают один и тот же порядковый номер, равный среднему арифметическому порядковых номеров, которые имели бы эти варианты до совпадения.
