Косвенные измерения в практике электрических измерений встречаются довольно часто. Вопрос оценки погрешности результата измерения – один из важнейших в таких экспериментах. Имея подробную исходную информацию о применяемых средствах измерения, измеряемых величинах и условиях проведения эксперимента, можно достаточно строго решить задачу оценки суммарной погрешности результата измерения. Правда, требуется четко оговаривать все допущения. Возможны два подхода к решению этой задачи: детерминированный и вероятностный, рассмотрим первый подход.
Детерминированный подход (иногда называемый методом наихудшего случая) более характерен для обычных технических измерений и экспресс-измерений с их обычно упрощенными моделями процессов и подходами. Перед рассмотрением этого подхода оговорим необходимые допущения:
а) инструменты исправны, имеют реальные погрешности, соответствующие своим классам точности. Причем их погрешности – только систематические, т.е. не меняющиеся в течение данного эксперимента. Случайных погрешностей нет;
б) исходные измеряемые величины характеризуются неизменными (в течение данного эксперимента) значениями основных параметров;
в) условия работы СИ – нормальные или рабочие;
г) функциональная зависимость искомой величины Y от исходных величин Хi, известна достаточно точно;
д) оператор имеет достаточную квалификацию.
Если интересующая нас величина Y связана с исходными величинами Хi, известной функциональной зависимостью F:
Y =F (X 1, X 2, …, Xn)
и предельные значения абсолютных погрешностей Δi – определения каждой исходной величины Хi известны, то предельное значение абсолютной погрешности Δ Y результата измерения искомой величины Y вобщем случае можно определить по так называемой формуле накопления частных погрешностей:
Δ Y = 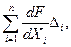
где dF/dXi – частные производные функционала F по каждой исходной величине в точках, соответствующих найденным значениям величин Xi;Δ i – предельные значения абсолютных погрешностей определения исходных величин Хi.
Рассмотрим два частных, но довольно распространенных, случая функциональной зависимости F.
Первый частный случай – функционал F имеет вид суммы. Если функциональная зависимость имеет вид
Y =  ,
,
где ai – коэффициенты функциональной зависимости, то предельное значение абсолютной погрешностиΔ Y определяется по формуле
Δ Y = 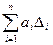 .
.
Относительная погрешность δ Y, %, при этом может быть найдена обычным образом:
δ Y = Δ Y / Y ´ 100.
Например, если Y= 5 Х1 + 2Х2 + Хъ, то ΔY = 5Δ1 + 2Δ2 + Δ3.
Второй частный случай – функционал F имеет вид произведения. Если функциональная зависимость имеет вид
Y = 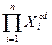 ,
,
где П – знак произведения п сомножителей; α i – коэффициенты – показатели степени исходных величин Xi,то предельное значение относительной погрешности δYопределяется по формуле
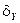 =
= 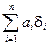 ,
,
где δ i – предельные значения относительных погрешностей определения исходных величин Xi.
Предельное значение абсолютной погрешности Δ Y затем находится обычным образом:
Δ Y = δ YY /100.
Например, если функционал Y имеет вид
Y = X 12 X 23/ X 35,
то значение относительной погрешности
δ Y = 2δ1 + 3δ2 + 5δ3.
И хотя формально третье слагаемое должно входить в сумму со знаком минус, но, поскольку предельные значения отдельных погрешностей практически всегда симметричны (±), то в худшем случае (самое неблагоприятное сочетание значений и знаков всех составляющих) предел общей погрешности есть сумма модулей отдельных составляющих.






