Погрешность результата измерения

Истинное значение измеряемой величины принципиально не может быть найдено (грамотный экспериментатор, понимая это, и не стремится к этому). Поэтому и реальное (истинное) значение погрешности результата определить не представляется возможным. И этого обычно не требуется. Вполне достаточно оперировать оцен­кой (приблизительным значением измеряемой величины) и диа­пазоном возможных значений погрешности. В случае простейшего детерминированного подхода (подхода по наихудшему случаю) используют предельное значение погрешности в каждом конкрет­ном случае, т.е. такое значение, превысить которое реальная по­грешность гарантированно не может.

Погрешность – довольно сложное и емкое понятие. Рассмотрим основные классификационные признаки погрешности результатов измерений.

Первый классификационный признак: что (кто) является при­чиной ошибки? Суммарная погрешность результата любого изме­рения в общем случае складывается из трех составляющих: инст­рументальной, методической и субъективной.

Инструментальная составляющая определяется основными мет­рологическими характеристиками собственно инструмента (т.е. СИ), его основной и дополнительной погрешностями.

Методическая составляющая погрешности результата измере­ния зависит от используемого метода измерения и не зависит от погрешности самого инструмента. Методическая погрешность мо­жет быть значительной, однако часто она может быть оценена или даже скомпенсирована (иногда практически полностью).

Субъективная составляющая не зависит ни от погрешности при­бора, ни от метода измерения, а в основном определяется квали­фикацией пользователя (субъекта). Эту погрешность не всегда можно предвидеть и заранее оценить. Эта составляющая может присут­ствовать в результате любого измерения.

Второй классификационный признак – способ выражения по­грешности. Абсолютная погрешность Δ – самая простая и понятная – это разность между измеренным Х иистин­ным Х _ист(или действительным Х _д,т. е. полученным более точным прибором) значениями измеряемой величины. Относительная погрешность δ – отношение абсолютной погрешно­сти к действительному Х _д(илиизмеренному X)значению, выра­женное в процентах.

Третий классификационный признак – зависимость погреш­ности (в абсолютном виде) от значения измеряемой величины X. Погрешности подразделяются на аддитивные, мультипликативные и погрешности линейности (рис. 1.7).

Аддитивной называется погрешность D_а, значения которой (бу­дучи представленными в абсолютной форме) не выходят за рам­ки независящего от значения измеряемой величины X коридора (см. рис. 1.7, а). Мультипликативной называется такая погрешность Δ_м, значения которой не выходят за рамки линейно зависящего от значения измеряемой величины X коридора (см. рис. 1.7, б). Любое другое поведение характерно для погрешности линейности D_л, ча­сто упрощенно называемой нелинейностью (см. рис. 1.7, в).

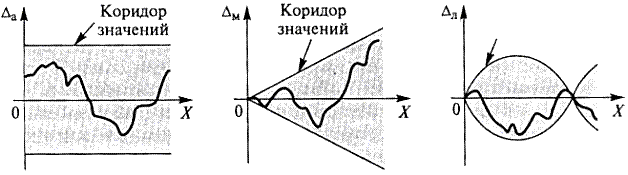
а б в

Рис.1.7. Зависимость погрешностей от значения измеряемой величины Х:

а – аддитивная погрешность, б – мультипликативная погрешность, в – погрешность линейности.

Четвертый классификационный признак – характер проявле­ния погрешности. Погрешности подразделяются на систематиче­ские и случайные. Систематическая – это такая погрешность, значение которой при повторении экспериментов неизменно или меняется по известному закону. Систематические погрешности, как правило, могут быть оценены и, следовательно, учтены путем введения поправок в результат измерения. Случайные – это такие погрешности, значения которых непредсказуемы. К случайным же относятся и различные промахи (сбои), которые объясняются или грубой ошибкой оператора, или кратковременной неисправ­ностью аппаратуры, или влиянием внешних электромагнитных полей. В случае многократных измерений влияние случайной по­грешности можно уменьшить обработкой полученных резуль­татов, например, нахождением их среднего арифметического значения.