| Вариант | Форма представления | Формула |
| Предел основной абсолютной погрешности | Δп = ±а | |
| Предел основной приведенной погрешности, % | γп = Δ/ Х н·100 = ±р | |
| Предел основной относительной погрешности, % | δп = Δ/ Х Д ·100 =±q | |
| Предел основной абсолютной погрешности | Δп = ± (а + bХ) | |
| Предел основной относительной погрешности | δп = ± [ c + d (X к/ X –1)] |
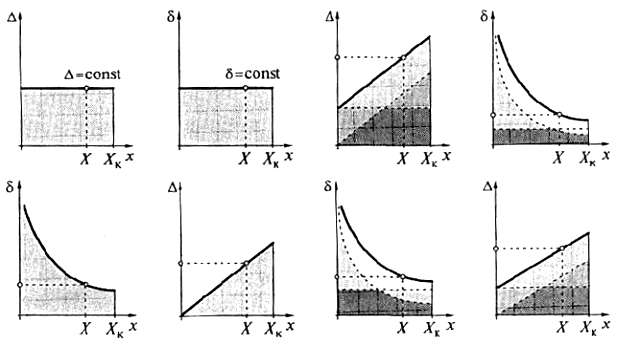
На рис. 1.9 приведена графическая иллюстрация разных способов задания классов точности. На рис. 1.9, а приведены варианты 1 и 2, на рис. 1.9, б приведен вариант 3, на рис. 1.9, в и рис. 1.9, г – соответственно варианты 4 и 5 из табл. 1.6. Для упрощения изображения на рис. 1.9 показаны не симметричные коридоры предельных значений погрешностей, а лишь их модули.
Классы точности простых измерительных приборов невысокой точности, например, щитовых стрелочных вольтметров, задаются пределом основной приведенной погрешности (вариант 2 из табл. 1.6). Для самопишущих приборов характерным является задание класса точности пределом основной относительной погрешности (вариант 3 из табл. 1.6). Для СИ средней и высокой точности применяются варианты 4 и 5 из табл. 1.6. Например, для мостов, компенсаторов, цифровых измерительных приборов, как правило, используется вариант 5 из табл. 1.6. Наиболее распространенной во всем мире (и одновременно наиболее понятной) формой задания погрешностей для современных цифровых СИ является вариант 4 из табл. 1.6.
При этом предел основной абсолютной погрешностиΔпсодержит и аддитивную (± а), и мультипликативную (±bХ)составляющие:
Δп = ±(a + bX),
где X –значение измеряемой величины; а и b – постоянные коэффициенты.
а б в г
Рис. 1.9. Графическая иллюстрация разных способов задания классов точности
На рис. 1.10, а приведена графическая иллюстрация аддитивной, мультипликативной составляющих и суммарной погрешности, представленных в абсолютном виде, а на рис. 1.10, б – иллюстрация этих составляющих и суммы, представленных в относительном виде.

а б
Рис. 1.10 Аддитивная, мультипликативная и суммарная погрешности в абсолютном (а) и относительном (б) виде
Форма задания класса точности пределом абсолютной погрешности, содержащей аддитивную и мультипликативную составляющие, может иметь несколько вариантов записи. Например, класс точности цифрового термометра может быть задан следующим образом:
Δп = ±(0,5 % результата + 2 единицы МЗР),
где МЗР – младший значащий разряд.
Здесь первое слагаемое – это мультипликативная погрешность, а второе – аддитивная.
Другой пример – цифровой мультиметр в режиме измерения переменных напряжений имеет класс точности, определяемый выражением
Δп = ±(1,0 % результата + 0,5 % диапазона измерения).
Для зарубежной аппаратуры (и для англоязычной литературы) характерна такая форма записи класса точности
Δп =±(аFS +bR),
где FS (Full Scale) – верхнее значение диапазона измерений; R (Reading) – результат измерения (отсчет); a, b – постоянные коэффициенты.






