Совокупность возможных значений случайной величины с вероятностями, отнесенными к этим значениям, образуют закон распределения случайной величины. В этом смысле каждая случайная величина подчинена определенному закону распределения. Форма задания, которого может быть различной. Простейшей формой задания такого закона для дискретных случайных величин является таблица, в которой перечислены в порядке возрастания возможные значения xi случайной величины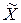 
и соответствующие им вероятности их появления pi:
| xi | x 1 | x 2 | ... | x n |
| pi | p 1 | p 2 | ... | p n |
Такая таблица называется статистическим рядом распределения случайной величины 
Пусть в результате наблюдений над случайной величиной 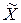получена выборка из N реализаций. Разделим весь диапазон значений случайной величины 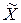на интервалы или «разряды» и подсчитаем количество значений mi, приходящихся на i -й разряд. Это число разделим на общее число наблюдений N и найдем частоту, соответствующую данному разряду:
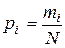(I.1)
Сумма частот всех разрядов равна единице.
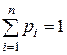, (I.2)
где n – число разрядов.
Построим статистический ряд (таблица 1). В первой строке таблицы приведены разряды в порядке их расположения вдоль оси абсцисс; во второй строке – количество попаданий m i значений случайной величины в данный интервал; в третьей – соответствующие частоты pi.
Таблица 1
| Ii | x min; x 1 | x 1; x 2 | ... | xi; xi +1 | ... | xn –1, x max |
| mi | m 1 | m 2 | ... | mi +1 | ... | mn |
| pi | p 1 | p 2 | ... | pi +1 | ... | pn |
Число разрядов, на которые следует группировать статистические данные, не должно быть большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Оптимальное число разрядов зависит от величины выборки и составляет 8-20. Длины разрядов могут быть как одинаковыми, так и различными.
Статистический ряд часто оформляется графически в виде гистограммы. При построении гистограммы по оси абсцисс откладываются разряды, и на каждом из разрядов как на их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника (рис. 1). В случае равных разрядов высоты прямоугольников пропорциональны соответствующим частотам. Полная площадь гистограммы равна единице.
Рис. 1. Эмпирический график плотности распределения p (xi) (гистограмма)
При увеличении числа опытов можно выбирать все более мелкие разряды. При этом гистограмма все более будет приближаться к некоторой кривой p (x), ограничивающей площадь, равную единице. Эта кривая называется плотностью распределения случайной величины Иногда функцию p (x) называют дифференциальным законом распределения величины Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями[1].
Основные свойства плотности распределения:
· плотность распределения есть неотрицательная функция: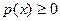 
;
· интеграл в бесконечных пределах от плотности распределения равен единице: 
.
Во многих практических задачах надежности вместо вероятности того, что случайная величина 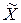принимает некоторое определенное значение xi, необходимо определить вероятность того, что случайная величина 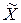не больше xi. Эта вероятность задается интегральной функцией распределения F (xi).
Для построения гистограммы интегральной функции распределения по оси абсцисс откладываются разряды, и на каждом i -м разряде строится прямоугольник, ордината которого равна сумме вероятностей p1 + p2 +...+ pi (рис. 2).
Для дискретной случайной величины
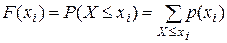(I.3)
Для непрерывной случайной величины
. (I.3)
Очевидно, что 
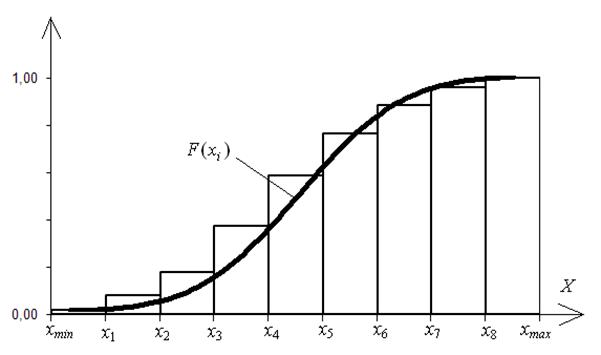
Рис. 2. Эмпирический график функции распределения F (xi)
Законы распределения случайной величины (интегральный и дифференциальный) являются исчерпывающей характеристикой случайной величины с вероятностной точки зрения. Однако во многих вопросах практики нет необходимости характеризовать случайную величину полностью, исчерпывающим образом. Зачастую достаточно бывает указать только отдельные числовые параметры, до некоторой степени, характеризующие существенные черты распределения случайной величины, например:
· среднее значение, около которого группируются возможные значения случайной величины;
· число, характеризующее степень разбросанности относительно среднего и т.д.
Пользуясь такими характеристиками, можно все существенные сведения относительно распределения случайной величины выразить более компактно с помощью минимального числа параметров. Такие характеристики, назначение которых - выразить в наиболее сжатой форме существенные особенности распределения, называются числовыми характеристиками случайной величины.
В теории вероятности и ее приложениях числовые характеристики и операции над ними играют огромную роль. С их помощью существенно облегчается решение многих вероятностных задач. Очень часто удается решить задачу до конца, оставляя в стороне законы распределения и оперируя одними числовыми характеристиками случайных величин.
