Вдоль оси волновода возникает бегущая волна в одном направлении. Из-за отражения симметричной волны, возникают стоячие волны. Перегородим волновод плоскостями  и
и  . Из-за отражения от этих торцевых поверхностей и вдоль
. Из-за отражения от этих торцевых поверхностей и вдоль  возникает бегущая стоячая волна. Принципы установления на торцах те же, что и на боковых поверхностях, т.е. равны нолю поперечная составляющая вектора
возникает бегущая стоячая волна. Принципы установления на торцах те же, что и на боковых поверхностях, т.е. равны нолю поперечная составляющая вектора  и нормальная составляющая вектора
и нормальная составляющая вектора  . На примере прямоугольного волновода мы видим, что продольные компоненты полей в волноводе имеют вид:
. На примере прямоугольного волновода мы видим, что продольные компоненты полей в волноводе имеют вид:
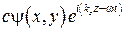
где  произвольная комплексная амплитуда.
произвольная комплексная амплитуда.  зависит от типа волны (ТМ и ТЕ, ТЕМ-волна), поэтому поле бегущей волны в положительном направлении
зависит от типа волны (ТМ и ТЕ, ТЕМ-волна), поэтому поле бегущей волны в положительном направлении  пропорционально
пропорционально  , а поле бегущее в отрицательном направлении пропорционально
, а поле бегущее в отрицательном направлении пропорционально  .
.
Для  -волны (ТЕ) граничные условия:
-волны (ТЕ) граничные условия:
 даст, что
даст, что 


В случае  -волны (ТМ) условия обращения в ноль
-волны (ТМ) условия обращения в ноль  на торцах волновода приводит к требованию
на торцах волновода приводит к требованию 
 нормальный контур производной от
нормальный контур производной от 
 , тогда
, тогда 
Т.о. в перегороженном волноводе величина  становится вместо непрерывной дискретной.
становится вместо непрерывной дискретной.
Поскольку  , то
, то
 , где
, где
 критическая частота
критическая частота  колебаний
колебаний
 - т.е. эта величина определяется тремя числами
- т.е. эта величина определяется тремя числами  и
и  , ее логично обозначать
, ее логично обозначать 
Периодический волновод имеет дискретный спектр частот. Вообще любая полость полностью изолированная от окружающего пространства обладает дискретным спектром частот, зависящих от геометрии полости, причем каждая частота определяется тремя числами. Такую полость называют резонатором, а собственные частоты – частотами резонатора. Резонаторы широко используются в качестве СВЧ.
Если бы стенки полости характеризовались проводимостью  (представим излучательный проводник), то поле бы в них не проникало и ЭМ энергия в резонаторе бы сохранялась. В действительности ЭМП проникает вглубь стенок резонатора и превращается в тепло, поэтому ЭМ энергия, запасенная в резонаторе постепенно уменьшается. Отношение энергии, запасенной в резонаторе и энергии теряемой за период колебаний обозначается
(представим излучательный проводник), то поле бы в них не проникало и ЭМ энергия в резонаторе бы сохранялась. В действительности ЭМП проникает вглубь стенок резонатора и превращается в тепло, поэтому ЭМ энергия, запасенная в резонаторе постепенно уменьшается. Отношение энергии, запасенной в резонаторе и энергии теряемой за период колебаний обозначается  и называется добротностью резонатора.
и называется добротностью резонатора.
Пусть  - энергия резонатора в момент времени
- энергия резонатора в момент времени 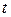 , то
, то  , т.е.
, т.е.  , где
, где  резонансная частота.
резонансная частота.
Т.о. поле в резонаторе изменяется не по закону  , а по закону
, а по закону  . Она может быть представлена в виде
. Она может быть представлена в виде  , где
, где  .
.
Энергия в интервале  очевидно пропорциональна
очевидно пропорциональна  . Легко убедится, что
. Легко убедится, что  . Интенсивность поля, как функция частоты имеет следующий вид:
. Интенсивность поля, как функция частоты имеет следующий вид:






