Рассмотрим простое падение плоской электромагнитной волны на границу раздела двух изотропных сред, характеризующихся параметрами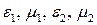 
. Векторы напряженности электромагнитного поля такой волны зависят от времени и радиус-вектора:
где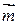 
― вектор рефракции, 
, 
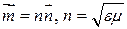― показатель преломления среды, 
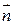― задает направление распространения волны.
Граничные условия:
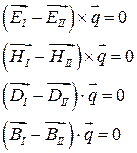
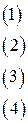
Полагаем, что поверхностная плотность зарядов и токов равны нулю,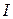 
и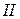 
относятся соответственно к первой и второй средам.
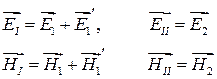
Из этих соотношений и из соотношения 
находим:
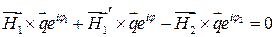
Так как векторные амплитуды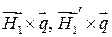 
и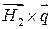 
постоянны, то ― линейное соотношение между экспоненциальными функциями, которые должны выполняться во всех точках границы раздела в любой промежуток времени. Но эти экспоненты с различными показателями линейно независимы. Значит, соотношение будет выполняться только при:
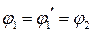
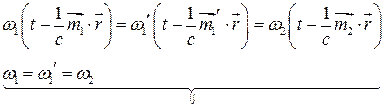
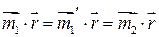
Перепишем выражение в виде:
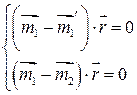
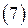
Выражение 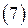справедливо только в точках границы, то есть при условии
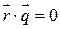
Сравнивая 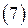и и учитывая, что в пределах границы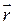 
― произвольный вектор, запишем выражение
,
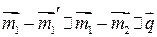которое можно переписать в виде:
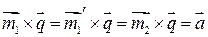
Умножая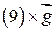 
и учитывая, что
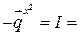1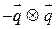 
― это оператор проектирования на плоскость границы раздела. Видим, что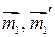 
и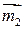 
лежат в одной плоскости, перпендикулярной 
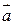, а также имеют одну и ту же проекцию на границу раздела:
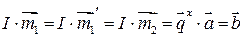
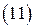
При этом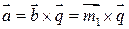 
(
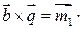(1 )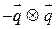 
)
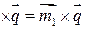Соотношения и 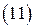позволяют записать геометрические законы отражения и преломления в форме:
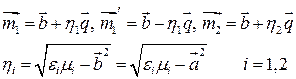
Пусть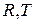 
― отражение и преломление
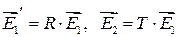
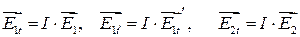
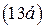
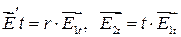
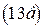
Из 
, и получим:
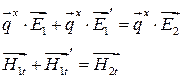
Введем понятие поверхностного импеданса 
плоской волны, по определению связывающее векторы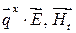 
:
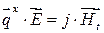
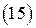
В изотропной среде:
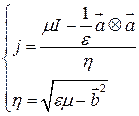
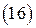
Учитывая, что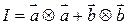 
, где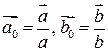 
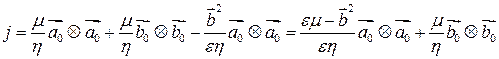
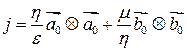
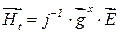
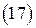
где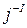 
― псевдообратный к оператору , то есть такой, что
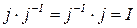
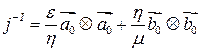― обратного не существует
Из находим:
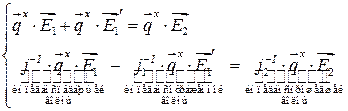
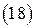
Исключая отсюда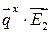 
, находим
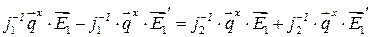
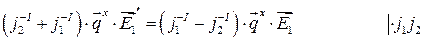
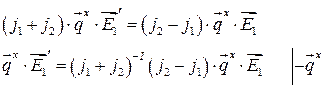
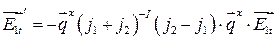
где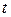 
― тангенциальная составляющая
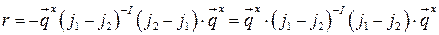
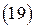
Аналогично исключая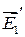 
:
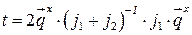
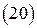
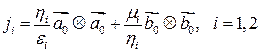
Подставляя в и и учитывая, что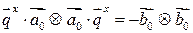 
, 
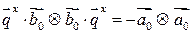, получим:
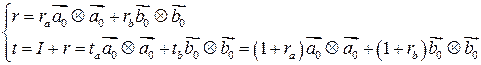
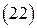
где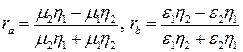 
Для полных напряженностей поля, чтобы найти операторы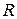 
и 
, воспользуемся условием ортогональности:
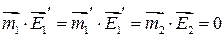
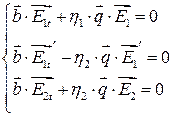
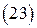
Умножая 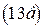на собственный вектор 
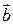и учитывая, что
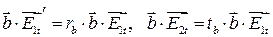
с помощью 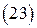находим, что
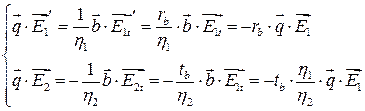
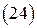
Учитывая, что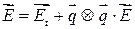 
, из и 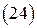находим:
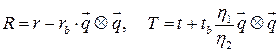
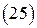
Окончательно формулы примут следующий вид
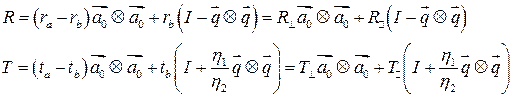
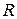и ― операторы отражения и пропускания для полных векторов.
