В проводящих средах наряду с уравнениями:

используются уравнения связи
 ,
,
именуемое законом Ома в дифференциальной форме.
Рассмотрим квазистационарное электромагнитное поле, которое удовлетворяет условию:
 ,
, 
где  ― период движения в системе,
― период движения в системе,  ― геометрическая протяженность области, в которой рассматриваются электромагнитные процессы.
― геометрическая протяженность области, в которой рассматриваются электромагнитные процессы.
При выполнении  можно считать, что значения полей в данной точке находятся в фазе с их значениями в любой другой точке системы.
можно считать, что значения полей в данной точке находятся в фазе с их значениями в любой другой точке системы.
Условие  обозначает, что частоты
обозначает, что частоты  должны быть достаточно низкими. При этом всегда выполняется условие
должны быть достаточно низкими. При этом всегда выполняется условие


― ещё одна форма условия квазистационарности (токи проводимости всегда больше токов смещения;  имеют то же значение, что и в постоянных полях).
имеют то же значение, что и в постоянных полях).
Условие квазистационарности выполняются в системах вплоть до инфракрасной области.
Пусть условие квазистационарности выполняется. Рассмотрим распределение тока по сечению однородного проводника


Отсюда



Такое же уравнение получится для магнитного поля. Это уравнение определяет зависимость от 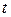 и
и 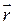 внутри проводника. На поверхности проводника имеют место обычные граничные условия.
внутри проводника. На поверхности проводника имеют место обычные граничные условия.
Рассмотрим случай тока, текущего внутри проводника по оси 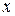 и изменяющегося по гармоническому закону:
и изменяющегося по гармоническому закону:


 не может зависеть от
не может зависеть от 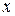 , так как в силу уравнений непрерывности
, так как в силу уравнений непрерывности  .
.
В соответствии с законом Ома ищем  в виде:
в виде:


Подставляя  в
в  , получим
, получим 
Его общее решение имеет вид

Или, если ввести обозначение  , то
, то

Так как  , то
, то


Напряженность электрического поля убывает экспоненциально вглубь проводника, уменьшаясь в  раз на расстоянии
раз на расстоянии  от поверхности.
от поверхности.


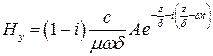
 и убывает по такому же закону, что и напряженность электрического поля.
и убывает по такому же закону, что и напряженность электрического поля.
Электромагнитное поле и соответственно весь ток локализован в тонком приповерхностном слое толщиной  ― скин-эффект.
― скин-эффект.
При  (случай постоянного тока)
(случай постоянного тока)  и скин-эффект исчезает. С другой стороны при
и скин-эффект исчезает. С другой стороны при  , то толщина скин-слоя стремится к нулю, то есть в идеальный проводник переменное поле не проникает. Скин-эффект становится более выраженным при переходе к высоким частотам. Результаты, полученные для упрощенной модели, имеют общий характер.
, то толщина скин-слоя стремится к нулю, то есть в идеальный проводник переменное поле не проникает. Скин-эффект становится более выраженным при переходе к высоким частотам. Результаты, полученные для упрощенной модели, имеют общий характер.






