Рассмотрим однородную изотропную среду, описываемую параметрами 
, 
, 
. Индекс 0 означает, что константы относятся к частоте 
. Пусть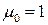 
, при этом следует полагать достаточно малой, иначе говорить о распространении волны неуместно. Тогда запишем уравнения Максвелла:
Отсюда находим волновые уравнения 
и 
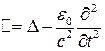
Будем искать решение уравнений в виде плоских монохроматических волн, распространяющихся вдоль оси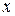 
Подставляя в для 
, например, находим
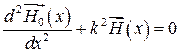
где 
Введем понятие комплексной диэлектрической проницаемости 
где 
― волновое число в вакууме
Согласно данному определению и формуле :
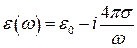
устанавливает связь между компонентами диэлектрической проницаемости и проводимостью среды.
Представим 
в следующем виде
и 
называют соответственно коэффициентом преломления и поглощения, то есть решение уравнения имеет следующий вид:
― комплексная амплитуда.
В случае произвольного направления распространения можно написать
где 
Связь между и из уравнений Максвелла
В отличие от случая распространения электромагнитных волн в вакууме:
однако как и в вакууме волны поперечные
Уравнения Максвелла в однородной изотропной среде допускает решение в виде плоских поперечных волн.
Они, вообще говоря, являются затухающими по экспоненциальному закону. Быстрота затухания определяется величиной , то есть мнимой частью комплексного показателя диэлектрической проницаемости.
Из и находим:
откуда
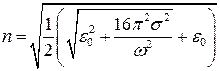
Знаки здесь выбраны так, чтобы и были вещественны, чтобы 
Формулы и определяют закон дисперсии в среде с проводимостью.
Если 
(то есть ток проводимости мал по сравнению с током смещения), то
Если 
, то среду называют прозрачной
Для такой среды
где 
― фазовая скорость распространения волны.
Последняя формула оправдывает название ― показатель преломления, ― так как показателем преломления называют 
в соответствии с формулой . Электромагнитные волны в непроводящей среде отличаются только скоростью распространения:
