Заряд является основной величиной, характеризующей свойства частиц, это скалярная величина, одинаковая во всех ИСО. Постоянство заряда сохраняется во всех известных физических экспериментах.
Закон сохранения заряда (уравнение непрерывности)
, (1)
должен быть справедлив в любой ИСО. Чтобы записать его в релятивистски инвариантной форме, введем 4-вектор
, (2)
Тогда (1) запишется в 4-х мерной форме
. (3)
Т.к.. (3) записано в четырехмерном виде и является релятивистским инвариантным выражением, то 
действительно 4-вектор и преобразуется при переходе от одной ИСО к другой по формулам преобразования Лоренца.
Пусть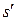 
некоторая СО, относительно которой заряды 
сосредоточенные в единице объема 
, покоятся. Система 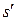движется со скоростью 
по отношению к системе s. Из формулы преобразования для 4-й компоненты 
вектора , учитывая, что 
в системе 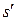, находим, что
, 
.
Так как 
, то
.
Таким образом, заряд любого элемента объёма является инвариантом преобразования Лоренца.
Релятивистски-инвариантная форма уравнений для потенциалов.
Система уравнений
, (1)
(2)
при учёте калибровки Лоренца
(3)
эквивалентна уравнениям Максвелла и справедлива во всех ИСО.
Релятивистская инвариантность (1), (2) становится очевидной, если заметить, что её без изменений можно записать в 4-х мерной форме.
Домножив (2) на i мы увидим, что правые части уравнений (1) и (2) содержат, соответственно, пространственные и временную компоненты 4-вектора 
. Значит, и левые части представляют компоненты некоторого 4-вектора, который называют 4-потенциалом
. (4)
С помощью 
и 
систему (1)-(2) можно объединить в одноЛоренц-инвариантное уравнение
, (5)
где
- оператор Даламбера. Условие калибровки преобретает вид
. (6)
Компоненты вектора 
не являются инвариантными величинами и преобразуются при переходе от одной ИСО к другой по общим правилам.
