Пусть в некоторой системе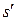 
покоится некоторое тело – масштаб, на который не действуют никакие силы. Обозначим через 
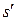- длину масштаба вдоль направления движения (оси x). Эту длину, т.е. длину, измеренную в той СО, в которой масщтаб покоится, будем называть собственной длиной масштаба. Пусть система движется со скоростью V относительно некоторой системы отсчёта s так, как это описано в предыдущем параграфе. Пусть в СО 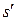координаты начала и конца масштаба равны 
и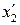 
. Так как масштаб движется относительно s, для измерения его размеров необходимо зафиксировать координаты его начала и конца в один и тот же момент времени. Пусть в момент времени t координаты начала и конца масштаба равны 
и 
. Тогда из преобразований Лоренца следует:
,
,
,
т.е.
, (1)
где l длина масштаба в системе s.
Следовательно l в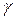 
раз меньше его собственной длины (лоренцево сокращение длины). Так как в направлении, перпендикулярном скорости размеры масштаба не изменяются, то объём масштаба V связан с его собственным объёмом 
формулой
. (2)
Длина и объём масштаба, не подверженного действию сил, которые могли бы вызвать его деформацию, имеют относительное значение, они различны в различных СО.
