Для системы заряженных частиц и поля рассмотрим изменение импульса частиц, находящихся в объеме V. Можем написать
(1)
Здесь 
- полный импульс частиц. Из уравнения Максвелла второй пары имеем: 
и 
Следовательно, 
Симметризуем в последним уравнении, прибавив в правой части к нулю выражение: 
Тогда имеем:
(2)
Рассмотрим интеграл следующего вида: 
Равенство: 
Вычитая одну формулу из другой получаем формулу:
Далее по теореме градиента: 
получаем, что
Учитывая симметрию 2-го интеграла формулы (2)отношение векторов 
и 
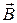получаем выражение:
(3)
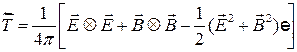(4)
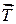- тензор Максвеловских натяжений.
Пусть вектор поля стремится к нулю при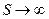 
быстрее чем 
, тогда поверхностный интеграл стремится к нулю.
Получаем, что 
(5)
Суммарный импульс системы состоящий из частицы поля сохраняется. Величина 
(6) - плотность импульса, т.е. (импульс единицы объема) электромагнитного поля.
Естественно, что 
(7) - импульс поля в объеме V.
Так согласно (5) имеет место закон сохранения суммарного импульса замкнутой системы. Передача импульса частицам сопровождается потерей импульса поля и наоборот.
В случае конечного объема V закон сохранения дается формулой (3), которую можно переписать в виде:
Пространстве 
- нормаль к поверхности поток импульса через единичную площадь из объема V сквозь S, т.е. сила действующая на единичную площадку поверхности.
Легко видеть, что между 
и вектором Пойтинга 
имеется связь:
