Рассмотрим замкнутую систему, состоящую из поля и частиц. Найдем работу W,произведение силами поля над частицами, находящиеся в объеме V. Относя эту работу W к единице времени t и считая заряды непрерывно распределенные в пространстве и пользуясь формулой плотности для силы Лоренца можем написать:
(1)
Учитывая, что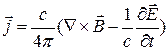 
Преобразуем формулу (1) к следующему виду:
(2)
Добавим к формуле (2) равную величину:
(Первое уравнение Максвелла)
и получим:
(3)
Используя векторное тождество: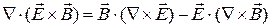 
Преобразуем первый интеграл в (3) к поверхностному.
(4)
Рассмотрим случай, когда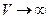 
. Если E и B стремится к нулю, при 
быстрее, чем по закону 
, то поверхностный интеграл обращается в ноль.
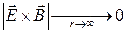быстрее, чем 
. А величина поверхности растет как 
. Следовательно (4) переходит в выражение: 
(5),
где 
(6)
Поскольку в левой части (5) стоит работа в единицу времени t, то правая – убыль энергии в единицу времени t. Естественно полагать,что в замкнутой системе, состоящей из поля и частиц, работа, производимая электромагнитным полем над частицами равна убыли энергии самого поля. При этом полю необходимо приписать энергию, плотность которой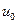 
выражается формулой (6). Выражение 
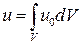нельзя свести к величинам, определяющимся только взаимным расположением и движением зарядов. Следовательно и нельзя считать потенциальную энергию взаимодействующих частиц. Плотность энергии, в частности, отлично от нуля в той области пространства, которая свободна от частиц. Наличие у электромагнитного поля энергии показывает, что оно не может рассматриваться как математическая фикция, т.е. делающая легким расчет между частицами взаимодействия. Поле столь же реально, что и частицы.
Рассмотрим теперь область поля имеющий конечный объем и ограниченной поверхностью S. Тогда уравнение (4), выражающее закон сохранения энергии показывает что убыль энергии в единицу времени t,т.е.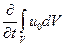 
, равна работе сил поля над зарядами и потоку 
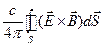, вытекающее через замкнутую поверхность S. Этот поток естественно интерпретировать, как поток энергии электромагнитного поля, вытекающая наружу через поверхность S из объема V.
Поток энергии является потоком энергии электромагнитного поля, так как он отличен от нуля и тогда, когда никакие частицы не пересекают поверхность и не уносят собой энергии.
Поток энергии электромагнитного поля характеризуется вектором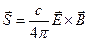 
(7), которой называют вектором Пойтинга. С учетом обозначений (6) и (7) уравнение (4) можно представить в виде:
(8)
Выражение (8) носит название теоремы Пойтинга.
Закон сохранения энергии в дифференциальной форме имеет вид:
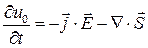(9)
В теории излучения встречаются поля убывающей с расстоянием по закону 
при . В этом случае 
к конечной величине. Физически это обозначает, что система, теряющая часть своей энергии, излучает.
