Пусть имеется изолированная система зарядов и электромагнитное поля в вакууме, и заданы начальные условия (значение положения, скорости, 
и 
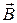зарядов). Пусть требуется определить и 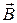во все последовательные моменты. Это можно решить синтезом уравнений Максвелла и классической механики. Определяем поле, силы, снова поле и т.д. Такая задача требует ограничений в постановке:
- внешние источники волн отсутствуют; система без излучения или на протяжении ограниченного времени, когда ни заряды, ни поля не выходят за пределы пространства;
- можно пренебречь силами радиционного трения;
- для описания движения зарядов необходима использовать механические модели тел, на которых заряды расположены (например, свободные точки 
). Для плотности зарядов и токов справедливо:
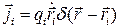
Обозначаем через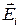 
, 
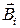поля, создаваемые зарядами/токами и используя уравнения Максвелла с учётом линейности операторов, получим
уравнение, описывающее систему зарядов и поля в виде:
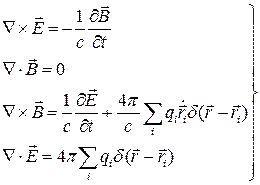(1)
в которых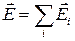 
, 
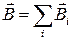определяют согласно принципу суперпозиции результирующего поля.
В (1) надо добавить уравнение движения материальных точек под действием силы Лоренца:
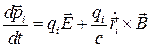(2)
Совокупность (1) – (2) называется уравнениями Максвелла-Лоренца для системы зарядов в вакууме.
Эти уравнения можно записать для непрерывности распределения заряда. Тогда вместо (1) будет обычные уравнения Максвелла, а в (2) импульс заменить на плотность импульса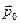 
:
(3)
Если заданы нелинейные уравнения, то уравнения Максвелла-Лоренца позволяют однозначно найти распределение электрических и магнитных полей в любой момент времени. Таким образом, справедлив принцип причинности.
Замечания: уравнения Максвелла-Лоренца применимы к макроскопической механической системы. Они неприменима к системе заряженных элементарных частиц.
