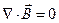 (1)
(1)
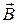 -соленоидальный. Его всегда можно положить равным ротору некоторый вспомогательный вектор
-соленоидальный. Его всегда можно положить равным ротору некоторый вспомогательный вектор  .
.
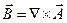 (2)
(2)
 - вспомогательный вектор, называемый вектор-потенциалом.
- вспомогательный вектор, называемый вектор-потенциалом.

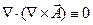
Подставим (2) в первое уравнение Максвелла:
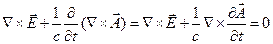
Откуда  .
.
Таким образом, 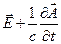 является потенциальным и его можно представить в виде:
является потенциальным и его можно представить в виде:
 (3)
(3)
 - некоторая скалярная функция координат и времени, названная скалярным потенциалом.
- некоторая скалярная функция координат и времени, названная скалярным потенциалом.
 нельзя представить в виде градиента от некоторой скалярной функции.
нельзя представить в виде градиента от некоторой скалярной функции.
Он имеет вихревой характер:
 (4)
(4)
причём  выражает закон электромагнитной индукции.
выражает закон электромагнитной индукции.
Если скалярный и векторный потенциалы введены, то уравнение первой группы Максвелла удовлетворяются тождественно.  и
и  определяются из уравнений второй группы Максвелла.
определяются из уравнений второй группы Максвелла.

Учитывая, что  , где
, где 
получаем:  (5)
(5)
 (6)
(6)
Потенциалы А и  – вспомогательные величины, введённые для упрощения, они не изменяют
– вспомогательные величины, введённые для упрощения, они не изменяют 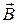 и
и  , но позволяют сделать (5) и (6) независимыми. Для однозначного знания поля
, но позволяют сделать (5) и (6) независимыми. Для однозначного знания поля  необходимо знать его ротор и дивергенцию. Но векторный потенциал А введён посредством (2), т.е. задан лишь ротор
необходимо знать его ротор и дивергенцию. Но векторный потенциал А введён посредством (2), т.е. задан лишь ротор  , а дивергенция – нет. Зададим её значение:
, а дивергенция – нет. Зададим её значение:
 (7) – соотношение Лоренца.
(7) – соотношение Лоренца.
Тогда (5) – (6) примут вид:
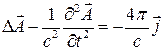 (8)
(8)
 (9)
(9)
Т.е. переменные разделились.
(8) – (9) эквивалентны исходным уравнениям Максвелла.
Если заданы 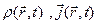 , удовлетворяют уравнениям непрерывности, то интегрирование (8),(9) даст
, удовлетворяют уравнениям непрерывности, то интегрирование (8),(9) даст  и
и  ,а
,а 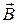 и
и  получим из (2),(4).
получим из (2),(4).
Уравнения типа  , где
, где  - заданная функция координат и времени называют уравнениями Даламбера.
- заданная функция координат и времени называют уравнениями Даламбера.
Вводя оператор Даламбера
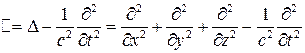
это уравнение записывают в компактной форме:
 (10)
(10)
Если  ,то (10) переходим в волновое уравнение:
,то (10) переходим в волновое уравнение:
 (11)
(11)
Если  ,
,  , (т.е. эти функции не зависят от времени), уравнение Пуассона:
, (т.е. эти функции не зависят от времени), уравнение Пуассона:
 (12)
(12)
С математической точки зрения, уравнения (10) – (12) проще уравнений Максвелла (в интегральной форме). Поэтому метод потенциалов представляет основной расчётный аппарат теории поля.
Калибровочная инвариантность потенциалов.
Определение потенциалов  и
и  является неоднозначным и допускает известный произвол. Обсудим вопрос о степени этого произвола. Из определения вектора-потенциала следовательно что если совершить преобразование:
является неоднозначным и допускает известный произвол. Обсудим вопрос о степени этого произвола. Из определения вектора-потенциала следовательно что если совершить преобразование:
 (1) где
(1) где  - произвольная функция, то мы придём к тому же значению
- произвольная функция, то мы придём к тому же значению 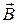 .
.

Таким образом,  . При этом для
. При этом для  получаем:
получаем:

Производя замену  (2), получим прежнее выражение для
(2), получим прежнее выражение для  , но уже через
, но уже через  и
и  .
.
Таким образом, вектор-потенциал определён с точностью до градиента произвольной функции  ,а скалярный потенциал до произвольной по t той же функции. В общем случае, два поля, описываемые потенциалами
,а скалярный потенциал до произвольной по t той же функции. В общем случае, два поля, описываемые потенциалами  ,
,  физически тождественны, если
физически тождественны, если  и
и  ,
,  и
и  могут быть связаны соотношениями (1)-(2). Иначе говоря, уравнения электродинамики неизменны, инвариантны по отношению к (1),(2).
могут быть связаны соотношениями (1)-(2). Иначе говоря, уравнения электродинамики неизменны, инвариантны по отношению к (1),(2).
Различные способы выбора  и
и  , оставляющие неизменными
, оставляющие неизменными  и
и 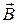 , называются различными калибровками потенциалов. Инвариантность
, называются различными калибровками потенциалов. Инвариантность  и
и 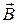 по отношению к калибровкам называют калибровочной/градиентной инвариантностью. (1) – (2) – калибровочные преобразованиями. Свойства калибровочной инвариантности подбирать потенциалы так, чтобы соотношения теории поля приняли максимально простой вид.
по отношению к калибровкам называют калибровочной/градиентной инвариантностью. (1) – (2) – калибровочные преобразованиями. Свойства калибровочной инвариантности подбирать потенциалы так, чтобы соотношения теории поля приняли максимально простой вид.
Например, соотношение Лоренца, отвечающие калибровке Лоренца. Убедимся, что такая калибровка всегда возможна.
Пусть для  ,
,  соотношение Лоренца не выполняется:
соотношение Лоренца не выполняется:

Произведём калибровочные преобразования: 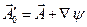 ,
, 
 (3)
(3)
 (4)
(4)
Условия Лоренца будут выполняется. Так как (4) будет выполнятся для любого  , то калибровка Лоренца всегда возможна.
, то калибровка Лоренца всегда возможна.
Произвольная функция  не определяется полностью уравнением (4). К ней можно добавить произвольную
не определяется полностью уравнением (4). К ней можно добавить произвольную  , такаю
, такаю  .
.
Совершая преобразование:  ,
, 
Приходим к тем же значением  и
и 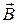 .
.
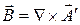

При этом  и
и 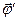 удовлетворяет условию Лоренца:
удовлетворяет условию Лоренца:

Поэтому можно подобрать  так, чтобы выполнялось ещё одно условие, налагаемое на
так, чтобы выполнялось ещё одно условие, налагаемое на  .
.






