Формула (5) из предыдущего параграфа выражает закон Эрстеда, установившего в 1820 – 1826 годах связь между электрическим током и магнитными явлениями. Из первого уравнения второй группы следует, что магнитное поле вызывается не только полями, но и переменным электрическим полем, т.к. даже при 
имеем
,
или в дифференциальной форме
.
Имеется двухсторонняя связь между электрическими и магнитными полями: переменное электрическое поле порождает магнитное поле, а переменное магнитное поле порождает электрическое поле.
Эта закономерность в домаксвелловскую эпоху обнаружена не была, поскольку слагаемое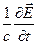 
обычно очень мало по сравнению с 
. Оба слагаемых могут иметь одинаковый порядок величины при периодическом изменении электрического поля с частотой 
Гц и выше. А это область радиочастот, не доступная физике 19-го века.
Правильно истолковав явление электромагнитной индукции: возникает электрическое поле при изменении магнитного, Максвелл предположил, что существует и обратный процесс: возникает магнитное поле при изменении электрического. Уравнение 
, не удовлетворяющее закону сохранения заряда, было дополнено слагаемым 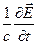, так что получившееся уравнение
(2)
(3)
удовлетворяло закону сохранения заряда. Величина была названа Максвеллом током смещения.
Схема рассуждений, приводящих к обобщению (2) может быть такой. Запишем (2) в следующем виде:
, (4)
где 
– неизвестный вектор.
Возьмём дивергенцию от обеих частей:
,
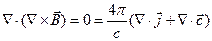т.е.
. (5)
Вектор дополняет 
таким образом, чтобы суммарная величина 
обладала свойствами соленоидального вектора. Из (5), требуя выполнения закона сохранения заряда и используя четвёртое уравнение Максвелла, получим
откуда следует, что
,
где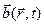 
– произвольный соленоидальный вектор.
Вообще говоря, нет оснований заранее считать 
, однако для получения симметрии между электрическими и магнитными полями полагают , что и приводит к знаменитому уравнению
.
