Связь между напряженностью 
и индукцией 
поля с одной стороны, и плотностью зарядов и токов с другой, в вакууме выражается в системой уравнений 1-го порядка в частных производных, называемых уравнениями Максвелла.
Впервые полная система уравнений была написана Максвеллом в виде уравнений для электромагнитного поля в веществе. Уравнения для электромагнитного поля в вакууме – частный случай при 
.
Система уравнений Максвелла играет роль исходных положений теории электромагнитного поля. Исторически она появилась как абстрактное обобщение эмпирических законов электромагнетизма: закона Кулона, закона полного тока, закона электромагнитной индукции Фарадея.
Запишем уравнения Максвелла в вакууме:
Уравнения (1) – (2) непосредственно применимы для изучения систем, состоящих из полей и зарядов в пустоте. Они неприменимы, если заряды расположены на телах, токи движутся по проводникам и т.д. Однако во многих случаях тела, определяющие положение зарядов и их движение, сами не влияют на поле. Например, магнитное поле линейного проводника с током можно рассчитывать, как поле соответствующего тока в вакууме.
Уравнения разделены на пары, чтобы подчеркнуть, что 2-е уравнение каждой пары следует из 1-го.
Действительно, если взять дивергенцию от обеих частей уравнения (1а), получим 
, т.е. 
во времени. Поскольку речь идет о произвольном переменном электромагнитном поле, то 
Аналогично, вычислив дивергенцию от (2а), получим
, (3)
или, учитывая уравнение непрерывности 
, 
, т.е. 
.
При другом подходе к уравнениям (1) – (2) можно не считать уравнение непрерывности независимым постулатом теории электричества. Его можно получить из уравнений Максвелла. Действительно, подставив (2б) в (3), получим: 
- а это и есть уравнение непрерывности.
Тем не менее, к системе уравнений (1) – (2) обычно добавляют пятое соотношение - уравнение непрерывности. При этом только первое уравнение каждой из пар можно считать независимым. Заметим, что в физике не всегда стремятся использовать минимальную систему исходных положений. Если связи между уравнениями выяснены, можно применять несколько избыточную, но физически содержательную систему уравнений. Например, уравнение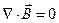 
истолковывают следующим образом: не существует в природе магнитных зарядов, создающих магнитное поле, подобно тому, как электрические заряды создают электрическое поле.
