Энергия магнитного поля. Замкнем цепь, содержащую индуктивность L и сопротивление R на источник с эдс ℇо. В контуре начнет возрастать ток, что приведет к появлению эдс самоиндукции Ɛs. По закону Ома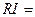 
ℇо + Ɛs, Þ ℇо = 
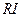- Ɛs. Источник с эдс ℇо за время dt совершит работу ℇоIdt. Умножим выражение в рамке на Idt
ℇоIdt = RI 2 dt - ƐsIdt.
Выражение RI 2 dt=δQ это джоулева теплота, а последнее слагаемое (- ƐsIdt = IdФ), так как по закону электромагнитной индукции Ɛs=-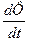 
. Из этого следует, что работа, которую совершает источник, больше, чем выделяющаяся теплота. Часть этой работы (IdФ) совершается против эдс самоиндукции и идет на увеличение энергии магнитного поля катушки индуктивности (соленоида). Так как 
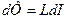, Þ
. (106)
Поскольку индуктивность соленоида 
, а индукция его магнитного поля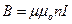 
, то энергию магнитного поля можно выразить как
= 
= 
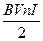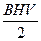. (107)
Мы учли, что 
(92), или, в данном случае однородного поля соленоида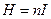 
. Энергия единицы объема (т.е. плотность энергии магнитного поля, 
) равна
= 
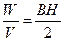. (108)
Для неоднородного магнитного поля плотность энергии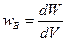 
, кроме того, расчет показывает, что выражение (108) верно и в векторном виде:
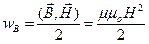. (109)
