Аналогичная ситуация возникает и при использовании свойства 3. Поэтому его также безопаснее применять в форме
или в форме 
.
При этом использование модулей также может привести к появлению посторонних корней за счёт расширения области определения уравнения.
Приведём примеры применения свойств 2 и 3 в процессе решения уравнений.
Пример 3. Решить уравнение 
1 способ.
Область определения данного уравнения D = (- ¥; - 3) È (0;+¥). Преобразуя левую часть уравнения по свойству 3, получим равносильную ему совокупность двух систем:
1 способ.
Далее
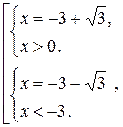
Первая система решений не имеет, 
решение второй системы.
Ответ: 
2 способ.
Преобразуем левую часть уравнения, используя модуль. Получим 
. Область определения данного уравнения при этом расширилась. Приведём подобные слагаемые, что опять приведёт к расширению области определения: 
Первый корень не принадлежит области определения данного уравнения.
Ответ: .
3 способ.
Воспользуемся свойством 2 справа налево. Получим систему, равносильную данному уравнению: 
решая которую, найдем корень 
.
Пример 4. Решить уравнение 
Данное уравнение равносильно системе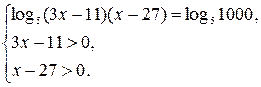 
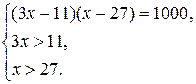
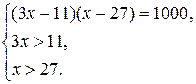
Решение системы х = 37.
Ответ: 37.
Пример 5. Решить уравнение 
Введём замену 3 х = t, t> 0. Данное уравнение примет вид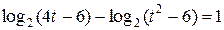 
, 
, 
,
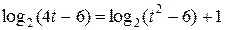Полученное уравнение равносильно системе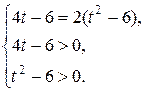 
Решим уравнение системы: 
Корень -1 не удовлетворяет условию t> 0, корень 3 удовлетворяет ему и является решением системы. Тогда 3 х = 3, х = 1.
Ответ: 1.
Свойство 4: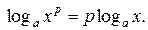 
Рассмотрим целые, чётные значения р (р =2 k, kÎ Z). Перепишем свойство в виде 
Допустимым значением переменной x в левой части равенства является любое действительное число, кроме нуля, в правой части равенства – положительное число. Следовательно, применение этого свойства в процессе решения уравнения изменяет его область определения, что может привести к потере решений (слева направо) или к приобретению посторонних (справа налево). Чтобы изменения области определения не происходило, свойство 4 слева направо используют в виде 
, а при его использовании справа налево необходима проверка принадлежности полученных корней области определения уравнения. Рассмотрим ряд примеров.
Пример 6. Решить уравнение 
Область определения данного уравнения задаётся системой неравенств
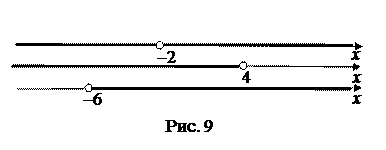
Таким образом, область определения данного уравнения
D=(-6;-2) È (-2;4). При 
данное уравнение равносильно уравнению 
решая которое, получим
Последнее уравнение имеет более широкую область определения, чем данное, поэтому возможно появление посторонних корней, но при они равносильны. Далее 
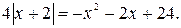На области определения данного уравнения D=(-6;-2)È(-2;4) последнее уравнение равносильно совокупности 
Выберем из найденных корней 
принадлежащие области определения D. Это 
Ответ: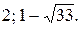 
Отметим, что отсутствие модуля привело бы к потере корня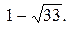 
Пример 7. Решить уравнение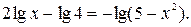 
Выполним преобразования данного уравнения, не меняющие его область определения 
Получим 
Применение свойства 4 справа налево приведёт к уравнению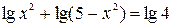 
с расширенной областью определения, что связано с ожиданием посторонних корней. Далее 
. Последнее уравнение имеет корни 
Из них области определения принадлежат 1и 2.
Ответ: 1; 2.
