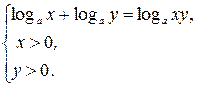4.1. Анализ преобразований
Преобразования логарифмов осуществляются посредством приведенных ниже основных свойств.
1. Если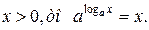 
2. Если х >0, у >0, то 
3. Если х >0, у >0, то 
4. Если 
5. Если х >0, то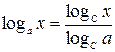 
(в частности, 
, 
).
Проанализируем перечисленные свойства с позиции влияния на область допустимых значений переменных х и у,если не ограничиваться рассмотрением их положительных значений.
Свойство 1: 
Очевидно, что применение первого свойства расширяет область допустимых значений переменной х, если использовать данное тождество «слева направо» и сужает её при использовании свойства «справа налево». Следовательно, при решении уравнений использование свойства 1 может привести либо к потере корней, либо к появлению посторонних. Чтобы не изменить область определения уравнения (сохранить равносильность) в процессе применения свойства 1, целесообразно воспользоваться такой формой его записи:
(слева направо), 
(справа налево).
Рассмотрим иллюстрирующие примеры.
Пример 1. Решить уравнение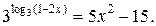 
Данное уравнение равносильно системе 
решая которую получим, 
х = -2 – решение системы.
Ответ: -2.
Пример 2. Решить уравнение 
.
Используя свойства степеней, получим 
.
Применение основного логарифмического тождества приведёт к уравнению 
с расширенной областью определения. Поэтому исходное уравнение равносильно системе 
Решим уравнение системы методом введения вспомогательного угла. Представим его в виде 
Разделим обе части уравнения на 
Тогда оно может быть записано в виде
, 
, 
Выберем среди полученных чисел решения системы, то есть числа, принадлежащие первой четверти. Ответ: 
Свойство 2: 
В левой части равенства переменные х и у могут принимать значения одного знака, а в правой – только положительные. Следовательно, применение свойства 2 в процессе решения уравнений меняет его область определения, что может привести к нарушению равносильности (потере или приобретению посторонних корней). Поэтому свойство 2 используется в форме 
или в форме 
. При этом область допустимых значений х и у расширяется до множества всех действительных чисел, кроме 0. Следовательно, в процессе решения уравнения могут появиться посторонние корни, которые отсеиваются проверкой их принадлежности области определения или подстановкой в данное уравнение. При использовании свойства справа налево следует сохранить область допустимых значений х и у, используя систему 
