Т.Е. Бондаренко
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ В ПРОЦЕССЕ РЕШЕНИЯ
УРАВНЕНИЙ
Учебное пособие по элементарной математике
Воронеж
УДК 512.3(075.8)
ББК 22.141.я7
Р е ц е н з е н т ы:
кандидат педагогических наук, почётный профессор кафедры информатики и методики преподавания математики (ВГПУ) Э.С. Беляева;
кандидат педагогических наук, доцент кафедры информатики и методики преподавания математики (ВГПУ) С.А. Титоренко
Бондаренко Т. Е.
Тождественные преобразования в процессе решения уравнений: учебное пособие по элементарной математике. – Воронеж: НАУКА – ЮНИПРЕСС, 2012. – 59с.
Настоящее учебное пособие посвящено использованию тождественных преобразований в процессе решения уравнений различных видов. Предметом исследования являются преобразования, изменяющие область определения уравнения, и, как следствие, приводящие к появлению посторонних корней или к их потере. Приводится анализ каждого преобразования, и рассматриваются средства, позволяющие сохранить равносильность уравнений. В книге содержатся многочисленные примеры решения уравнений, а также задания для самостоятельной работы учащихся.
Пособие предназначено для обеспечения курса элементарной математики в педагогическом вузе. Оно может быть использовано учителями средних общеобразовательных учреждений в процессе обучения математике, для подготовки учащихся к единому государственному экзамену или для проведения элективного курса в условиях профильного обучения.
© Бондаренко Т. Е., 2012
Содержание
Предисловие................................................ 4
I. Тождественные преобразования и равносильность уравнений...... 6
II.Тождественные преобразования, изменяющие область определения
уравнения................................................ 8
1. Приведение подобных слагаемых............................ 8
1.1. Анализ преобразования................................... 8
1.2. Комплекс заданий.......................................... 10
2. Сокращение дробей........................................ 11
2.1. Анализ преобразования......................................11
2.2. Комплекс заданий..........................................14
3. Преобразования корней арифметических корней............... 15
3.1. Анализ преобразований..................................... 15
3.2. Комплекс заданий.......................................... 32
4. Преобразования логарифмов................................ 35
4.1. Анализ преобразований.................................... 35
4.2. Комплекс заданий.......................................... 44
5. Преобразование тригонометрических выражений............... 46
5.1. Анализ преобразований..................................... 46
5.2. Комплекс заданий.......................................... 51
Приложение. Основные понятия и теоремы....................... 53
Литература................................................... 59
Предисловие
Изучение математики тесно связано с решением уравнений. Этот процесс иногда приводит к удивительным результатам. Казалось бы решение выполнено верно, но имеющийся в учебнике ответ не совпадает с полученным. Приведём примеры.
Решим уравнение 
(1) [2, № 5.110, с. 87]. Умножим обе части данного уравнения на сопряжённое выражение 
.
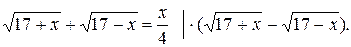
Получим уравнение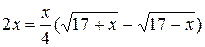 
(2). Очевидно, что х = 0 – корень уравнения (2). Приведём его к виду 
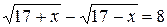и сложим с данным уравнением (1), тогда получим уравнение 
, решая которое найдём корни х = -8, х = 8. Подстановкой в данное уравнение убеждаемся, что -8, 0, 8 - посторонние корни данного уравнения.
Рассмотрим ещё один пример. Решим уравнение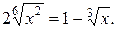 
Используя свойство арифметических корней, получим уравнение 
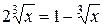, имеющее корень 
Однако очевидно, что и число -1 является потерянным корнем данного уравнения.
Таким образом, иногда решение уравнения может привести к появлению посторонних корней или к их потере. Возникает вопрос, почему это происходит? В настоящем пособии приводится подробный ответ на этот вопрос для случая, когда выполняются тождественные преобразования выражений, входящих в данное уравнение. В нём перечислены преобразования, выполнение которых может привести к изменениям множества корней уравнения, и описаны средства, позволяющие сохранить его. Пособие содержит многочисленные примеры с решениями и упражнения для самостоятельной работы учащихся.
Уравнения, в которых могут появиться посторонние решения или происходит их потеря представлены в различных литературных источниках. Некоторые из них приведены в списке литературы. Особенно интересные задания включены из книг [1], [2], [3]. Однако отличительной особенностью данного пособия является его тематическая направленность и систематизация учебного материала.
Автор выражает благодарность рецензентам Э.С.Беляевой, С.А Титоренко за участие в совершенствовании пособия и надеется, что оно послужит повышению качества математической подготовки студентов и школьников.
Тождественные преобразования и равносильность уравнений
Решение данного уравнения – это процесс, состоящий в переходе к другим уравнениям до тех пор, пока не будет получено уравнение с очевидными корнями. Такие переходы осуществляются посредством различных преобразований. При этом одни преобразования приводят к уравнению с такими же корнями (равносильному данному), другие - не обладают таким свойством. Напомним, что два уравнения f1(x)=g1(x) и f2(x)=g2(x) называются равносильными (эквивалентными) на множестве М, если они имеют одни и те же решения, принадлежащие этому множеству. Преобразования, сохраняющие решения, изучаются в теории равносильных уравнений. Основное содержаниеэтой теории составляют теоремы, гарантирующие замену данного уравнения ему равносильным. Наряду с основными понятиями они приведены в приложении к настоящему курсу (с.49). Особый интерес представляет для нас теорема 1. Приведём её формулировку: если в уравнении f1(x)=g1(x) выполнить тождественное преобразование выражений f1(x) или (и) g1(x), по формуле, не меняющей область определения данного уравнения D, то получится уравнение f2(x)=g2(x), равносильное данному уравнению на множестве D.
Например, в соответствии с теоремой 1 уравнения х 3 + 3 х 2 - 4 х- 12 = 0и(х+ 3)(х- 2)(х+ 2) = 0 равносильны на множестве всех действительных чисел, а уравнения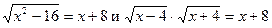 
не равносильны, так как х=- 5, являясь корнем первого уравнения, не является корнем второго уравнения. Причина нарушения равносильности состоит в том, что в результате выполненного преобразования по формуле 
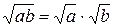изменилась (сузилась) область определения данного уравнения, что привело к потере корня.
Докажем теорему 1 учитывая, что каждое уравнение вида f(x)=g(x) может быть приведено к виду F(x)=0.
Дано: уравнение F1(x) = 0 (1) с областью определения D,
р – формула (тождество), посредством которого выполняется преобразование выражения F1(x), не изменяющая D,
F2(x) = 0 (2) – уравнение, полученное из данного уравнения в результате преобразования.
Доказать: уравнения (1) и (2) равносильны.
Доказательство
Пусть х 1 – корень уравнения (1), тогда x 1ÎD и F1(x 1) = 0 – истинное числовое равенство. В результате применения тождества р выражение F1(x) примет вид F2(x). Область определения D не изменилась, то есть F2(x 1) имеет смысл. По определению тождественно равных выражений F2(x 1) = F1(x 1), то есть F2(x 1) = 0 – истинное числовое равенство, следовательно, x 1 – корень уравнения (2).
Обратно. Пусть х 2 – корень уравнения (2), тогда x 2ÎD и F2(x 2) = 0 – истинное числовое равенство. В результате применения тождества р выражение F2(x) примет вид F1(x). Область определения D не изменилась, то есть F1(x 2) имеет смысл. По определению тождественно равных выражений F1(x 2) = 0 – истинное числовое равенство, что означает x 2 – корень уравнения (1). Равносильность доказана.
Таким образом, с преобразованиями, не изменяющими области определения данного уравнения, ситуация ясна. Однако открытым остаётся вопрос, как действовать, если тождественное преобразование меняет область определения данного уравнения. При этом оно может расширить её, и тогда возможны посторонние корни, либо сузить, что может привести к потере корней.
Выявим и исследуем тождественные преобразования, обладающие свойством расширять или сужать область определения уравнения, и определим для них средства сохранения равносильности уравнений.